Advertisements
Advertisements
Question
त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए।
संगत जीवा द्वारा बनाए गए वृत्तखंड का क्षेत्रफल [ प्रयोग कीजिए =`22/7`]
Solution 1
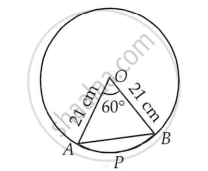
खंड APB का क्षेत्रफल = [क्षेत्र AOB का क्षेत्रफल] − [ΔAOB का क्षेत्रफल] ....(1)
AOB में, OA = OB = 21 सेमी
∴ ∠A = ∠B = 60° ...(∴ ∠O = 60°)
AOB एक समबाहु त्रिभुज है।
∴ AB = 21 cm
ΔOAB का क्षेत्रफल = `sqrt3/4 xx ("भुजा")^2` ......[∴ ΔAOB एक समबाहु त्रिभुज है]
`= sqrt3/4 xx 21 xx 21 "cm"^2`
= `(441sqrt3)/4 "cm"^2` ....(2)
(1) में भाग (ii) और (2) का उपयोग करके, हमारे पास है,
खंड का क्षेत्रफल = `[231 "cm"^2] − [(441sqrt3)/4 "cm"^2]`
`= (231 - (441sqrt3)/4) "cm"^2`
Solution 2

क्षेत्र OACB का क्षेत्रफल = `(60^@)/(360^@)xxpir^2`
`= 1/6xx22/7xx21xx21`
= 231 cm2
In ΔOAB,
∠OAB = ∠OBA (As OA = OB)
∠OAB + ∠AOB + ∠OBA = 180°
2∠OAB + 60° = 180°
∠OAB = 60°
अतः ΔOAB एक समबाहु त्रिभुज है।
ΔOAB का क्षेत्रफल = `sqrt3/4 xx ("Side")^2`
`= sqrt3/4 xx (21)^2 = (441sqrt3)/4 "cm"^2`
`= (231 - (441sqrt3)/4) "cm"^2`
RELATED QUESTIONS
एक घड़ी की मिनट की सुई की लंबाई 14 सेमी है। इस सुई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए। `[pi = 22/7 "का प्रयोग करें"]`
12 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 120° का कोण अंतरित करती है। वृत्त के संगत वृत्त खण्ड का क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73 ` का प्रयोग कीजिए।]
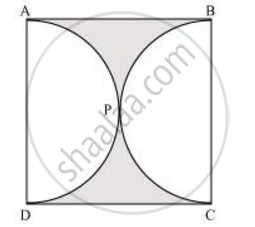
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि ABCD भुजा 14 सेमी का एक वर्ग है तथा APD और BPC दो अर्धवृत्त हैं। [उपयोग Π = `22/7`]
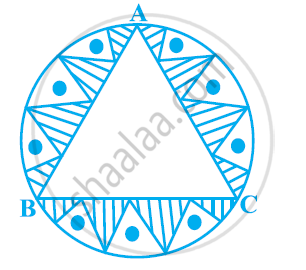
एक वृत्ताकार मेजपोश, जिसकी त्रिज्या 32 सेमी है, में बीच में एक समबाहु ABC त्रिभुज छोड़ते हुए एक डिजाइनर बना हुआ है, जैसा कि आकृति में दिखाया गया है। इस छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = 22/7]
क्या यह कहना सत्य है कि एक वृत्तखंड का क्षेत्रफल संगत त्रिज्यखंड के क्षेत्रफल से कम होता है? क्यों?
यदि त्रिज्या r वाले एक वृत्त के एक चाप की लंबाई त्रिज्या 2r वाले एक वृत्त के चाप की लंबाई के बराबर हो, तो पहले वृत्त के संगत त्रिज्यखंड का कोण दूसरे वृत्त के संगत त्रिज्यखंड के कोण का दोग़ना होता है? क्या यह कथन असत्य है? क्यों?
त्रिज्या 14 cm वाले एक वृत्त के लघु वृत्तखंड का क्षेत्रफल ज्ञात कीजिए, जिसके संगत त्रिज्यखंड का कोण 60° है।
एक 20 cm लंबे तार के टुकड़े को मोड़कर एक वृत्त का चाप बनाया गया है, जो इस वृत्त के केंद्र पर 60° का कोण अंतरित करता है। वृत्त की त्रिज्या ज्ञात कीजिए।
त्रिज्या 5 cm वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए जिसके संगत चाप की लंबाई 3.5 cm है।
10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
संगत दीर्घ त्रिज्यखंड [प्रयोग कीजिए = 3.14]
