Advertisements
Advertisements
प्रश्न
त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए।
संगत जीवा द्वारा बनाए गए वृत्तखंड का क्षेत्रफल [ प्रयोग कीजिए =`22/7`]
उत्तर १
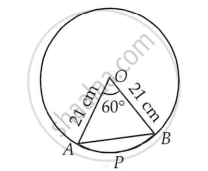
खंड APB का क्षेत्रफल = [क्षेत्र AOB का क्षेत्रफल] − [ΔAOB का क्षेत्रफल] ....(1)
AOB में, OA = OB = 21 सेमी
∴ ∠A = ∠B = 60° ...(∴ ∠O = 60°)
AOB एक समबाहु त्रिभुज है।
∴ AB = 21 cm
ΔOAB का क्षेत्रफल = `sqrt3/4 xx ("भुजा")^2` ......[∴ ΔAOB एक समबाहु त्रिभुज है]
`= sqrt3/4 xx 21 xx 21 "cm"^2`
= `(441sqrt3)/4 "cm"^2` ....(2)
(1) में भाग (ii) और (2) का उपयोग करके, हमारे पास है,
खंड का क्षेत्रफल = `[231 "cm"^2] − [(441sqrt3)/4 "cm"^2]`
`= (231 - (441sqrt3)/4) "cm"^2`
उत्तर २

क्षेत्र OACB का क्षेत्रफल = `(60^@)/(360^@)xxpir^2`
`= 1/6xx22/7xx21xx21`
= 231 cm2
In ΔOAB,
∠OAB = ∠OBA (As OA = OB)
∠OAB + ∠AOB + ∠OBA = 180°
2∠OAB + 60° = 180°
∠OAB = 60°
अतः ΔOAB एक समबाहु त्रिभुज है।
ΔOAB का क्षेत्रफल = `sqrt3/4 xx ("Side")^2`
`= sqrt3/4 xx (21)^2 = (441sqrt3)/4 "cm"^2`
`= (231 - (441sqrt3)/4) "cm"^2`
संबंधित प्रश्न
10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
संगत लघु वृत्तखंड [प्रयोग कीजिए π = 3.14]
दो वृत्तों की परिधियाँ बराबर हैं। क्या यह आवश्यक है कि इन वृतों के क्षेत्रफल भी बराबर हों? क्यों?
दो वृत्तों के क्षेत्रफल बराबर हैं। क्या यह आवश्यक है कि इन वृत्तों की परिधियाँ भी बराबर हों? क्यों?
विमाओं 20 m × 16 m वाले एक आयताकार खेत के कोने पर एक गाय 14 m लंबी रस्सी से बँधी हुई है। खेत का वह क्षेत्रफल ज्ञात कीजिए जिसमें गाय चर सकती है।
किसी वृत्ताकार खेल के मैदान का क्षेत्रफल 22176 m2 है। इस मैदान पर 50 रु प्रति मीटर की दर से बाड़ लगवाने का व्यय ज्ञात कीजिए।
बराबर त्रिज्या 3.5 cm वाले तीन वृत्त इस प्रकार खींचे गये हैं कि इनमें से प्रत्येक अन्य दो वृत्तों को स्पर्श करता है। इन वृत्तों से परिबद्ध क्षेत्रफल ज्ञात कीजिए।
त्रिज्या 5 cm वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए जिसके संगत चाप की लंबाई 3.5 cm है।
त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए।
चाप द्वारा बनाए गए त्रिज्यखंड का क्षेत्रफल [प्रयोग कीजिए =`22/7`]
