Advertisements
Advertisements
प्रश्न
उत्तर
वृत्ताकार तालाब की त्रिज्या r1 = `17.5/2` m = 8.75 m
पथ की चौड़ाई = 2 m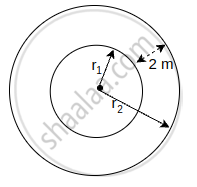
तालाब सहित पथ की त्रिज्या
r2 = 8.75 + 2 = 10.75 m
पथ का क्षेत्रफल = `pi"r"_2^2 - pi"r"_1^2 = pi["r"_2^2 - "r"_1^2]`
पथ के निर्माण की लागत = रु 25 `pi("r"_2^2 - "r"_1^2)`
∴ आवश्यक लागत = रु `25 xx 22/7 [(10.75)^2 - (8.75)^2]`
= `25 xx 22/7 [10.75 - 8.75][10.75 + 8.75]`
= `25 xx 22/7 xx 2 xx 19.5`
= `(50 xx 22 xx 19.5)/7`
= `(1100 xx 19.5)/7`
= `21450/7`
= रु. 3064.29
अत: पथ निर्माण की लागत 3064.29 रुपये है।
APPEARS IN
संबंधित प्रश्न
एक वृत्त, के चतुर्थांश का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22 सेमी है। `[pi = 22/7 "का प्रयोग करें"]`
15 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 60° का कोण अंतरित करती है। वृत्त के संगत लघु और प्रमुख खण्डों के क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73`]
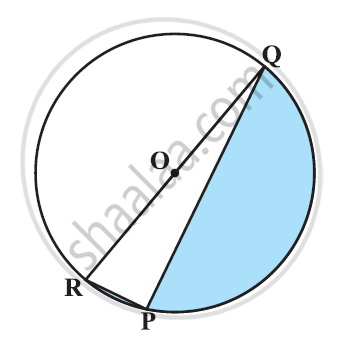
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि PQ = 24 सेमी, PR = 7 सेमी तथा O वृत्त का केंद्र है। [उपयोग Π = `22/7`]
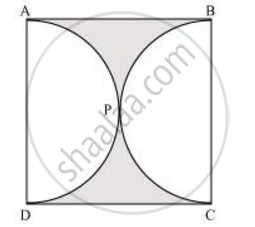
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि ABCD भुजा 14 सेमी का एक वर्ग है तथा APD और BPC दो अर्धवृत्त हैं। [उपयोग Π = `22/7`]
यदि R1 और R2 त्रिज्याओं वाले दो वृत्तों की परिधियों का योग त्रिज्या R वाले एक वृत्त की परिधि के बराबर हो, तो ______।
क्या यह कहना सत्य है कि व्यास d cm वाले एक वृत्ताकार पहिए द्वारा एक परिभ्रमण में चली गयी दूरी 2 π d cm होती है? क्यों?
दो भिन्न वृत्तों के बराबर लंबाइयों वाले चापों के संगत त्रिज्यखंडों के क्षेत्रफल बराबर होते हैं। क्या यह कथन सत्य है? क्यों?
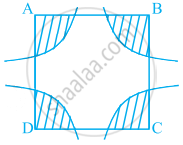
आकृति में, चतुर्भुज ABCD के A, B, C और D शीर्षों को केंद्र मानकर और 21 cm की त्रिज्या लेकर चाप खींचें गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वृत्त की उस जीवा द्वारा निर्मित दोनों वृत्तखंडों के क्षेत्रफलों का अंतर ज्ञात कीजिए, जिसकी लंबाई 5 cm है और जो केंद्र पर 90∘ का कोण अंतरित करती है।
त्रिज्या 21 cm वाले एक वृत्त के 120∘ कोण वाले त्रिज्यखंड और उसके संगत दीर्घ त्रिज्यखंड के क्षेत्रफलों का अंतर ज्ञात कीजिए।
