Advertisements
Advertisements
प्रश्न
15 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 60° का कोण अंतरित करती है। वृत्त के संगत लघु और प्रमुख खण्डों के क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73`]
5 cm त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर 60° का कोण अंतरित करती है। संगत लघु और दीर्घ वृत्तखंडों के क्षेत्रफल ज्ञात कौजिए। [π = 3.14 और `sqrt3 = 1.73` का प्रयोग कीजिए।]
उत्तर
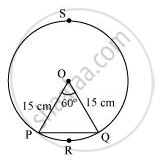
वृत्त की त्रिज्या (r) = 15 सेमी
त्रिज्यखंड OPRQ का क्षेत्रफल = `60^@/360^@xxpir^2`
= `1/6 xx 3.14 xx (15)^2`
= 117.75 सेमी2
ΔOPQ में,
∠OPQ = ∠OQP (As OP = OQ)
∠OPQ + ∠OQP + ∠POQ = 180°
2 ∠OPQ = 120°
∠OPQ = 60°
ΔOPQ एक समबाहु त्रिभुज है।
∠OPQ का क्षेत्रफल = `(sqrt3)/4 xx (r)^2`
= `sqrt3/4 xx (15)^2`
= `(225sqrt3)/4 "सेमी"^2`
= `56.25sqrt3`
97.3125 सेमी2
खंड PRQ का क्षेत्रफल = त्रिज्यखंड ΔPRQ का क्षेत्रफल − OPQ का क्षेत्रफल
= 117.75 − 97.3125
= 20.4375 सेमी2
वृहत खंड PSQ का क्षेत्रफल = वृत्त का क्षेत्रफल − खंड PRQ का क्षेत्रफल
= πr2 − 20.4375
= π × (15)2 − 20.4375
= 3.14 × 225 − 20.4375
= 706.5 − 20.4375
= 686.0625 सेमी2
APPEARS IN
संबंधित प्रश्न
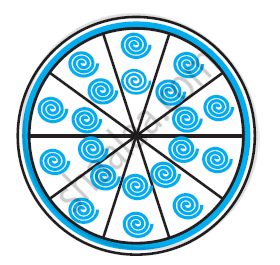
एक वृत्ताकार ब्रूच को चाँदी के तार से बनाया जाना है जिसका व्यास 35 मिमी है। तार को वृत्त के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्यखंडों में विभाजित करता है जैसा कि आकृति में दर्शाया गया है। तो ज्ञात कीजिए:
- कुल वांछित चाँदी के तार की लंबाई
- ब्रूच के प्रत्येक त्रिज्यखंड का क्षेत्रफल [उपयोग π = `22/7`]
यदि R1 और R2 त्रिज्याओं वाले दो वृत्तों की परिधियों का योग त्रिज्या R वाले एक वृत्त की परिधि के बराबर हो, तो ______।
व्यासों 36 cm और 20 cm वाले दो वृत्तों की परिधियों के योग के बराबर परिधि वाले एक वृत्त की त्रिज्या ______ है।
s मीटर की दूरी चलने के लिए, त्रिज्या r मीटर वाला एक वृत्ताकार पहिया `s/(2πr)` चक्कर लगाता है। क्या यह कथन सत्य है? क्यों?
दो भिन्न वृत्तों के बराबर लंबाइयों वाले चापों के संगत त्रिज्यखंडों के क्षेत्रफल बराबर होते हैं। क्या यह कथन सत्य है? क्यों?
एक मोटर साइकिल के पहिये की त्रिज्या 35 cm है। 66 km/h की चाल रखने के लिए, पहिये को प्रति मिनट कितने चक्कर लगाने चाहिए?
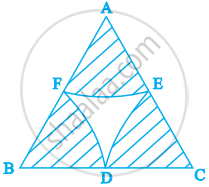
आकृति में, 10 cm भुजा वाले एक समबाहु त्रिभुज के शीर्षों A, B और C को केंद्र लेकर चाप खींचे गये हैं, जो परस्पर क्रमश: BC, CA और AB के मध्य बिंदुओं D, E और F पर प्रतिच्छेद करते हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए (π = 3.14 का प्रयोग कीजिए)।
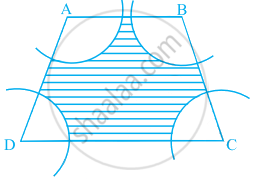
आकृति में, ABCD एक समलंब है, जिसमें AB || DC, AB = 18 cm, DC = 32 cm तथा AB और DC के बीच की दूरी = 14 cm है। यदि A, B, C और D को केंद्र मानकर त्रिज्याओं 7 cm के चाप खींचे गये हैं, तो इस आकृति के छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
त्रिज्या 5 cm वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए जिसके संगत चाप की लंबाई 3.5 cm है।
