Advertisements
Advertisements
प्रश्न
उत्तर
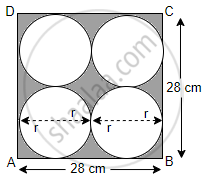
माना a वर्ग ABCD की भुजा है।
वर्ग ABCD का क्षेत्रफल = 784 cm2
⇒ a2 = 784
⇒ a = `sqrt(784)`
= `sqrt(2 xx 2 xx 2 xx 2 xx 7 xx 7)`
= 2 × 2 × 7
⇒ a = 28 cm
अब, चार वृत्तों में,
4r = AB
⇒ 4r = 28 cm
⇒ r = 7 cm
वृत्तों और वर्गों के बीच घिरा क्षेत्र
= वर्ग का क्षेत्रफल – 4 वृत्तों का क्षेत्रफल
= 784 – 4πr2
= `784 - 4 xx 22/7 xx 7 xx 7`
= 784 – 616
= 168 cm2
अतः, वृत्ताकार प्लेटों से न ढकी वर्गाकार शीट का क्षेत्रफल 168 cm2 है।
APPEARS IN
संबंधित प्रश्न
15 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 60° का कोण अंतरित करती है। वृत्त के संगत लघु और प्रमुख खण्डों के क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73`]
12 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 120° का कोण अंतरित करती है। वृत्त के संगत वृत्त खण्ड का क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73 ` का प्रयोग कीजिए।]
यदि R1 और R2 त्रिज्याओं वाले दो वृत्तों की परिधियों का योग त्रिज्या R वाले एक वृत्त की परिधि के बराबर हो, तो ______।
s मीटर की दूरी चलने के लिए, त्रिज्या r मीटर वाला एक वृत्ताकार पहिया `s/(2πr)` चक्कर लगाता है। क्या यह कथन सत्य है? क्यों?
त्रिज्या 28 cm वाले एक वृत्त के उस त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका केंद्रीय कोण 45° है।
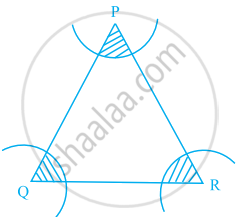
आकृति में, 14 cm की त्रिज्याएँ लेकर तथा P, Q और R को केंद्र मान कर चाप खींचे गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
बराबर त्रिज्या 7 cm त्रिज्या वाले चार वृत्ताकार गत्ते के टुकड़ों को एक कागज पर इस प्रकार रखा गया है कि प्रत्येक टुकड़ा अन्य दो टुकड़ों को स्पर्श करता है। इन टुकड़ों के बीच में परिबद्ध भाग का क्षेत्रफल ज्ञात कीजिए।
किसी कमरे के फर्श की विमाएँ 5 m × 4 m हैं और इस पर वृत्ताकार टाइलें लगायी जाती हैं, जिनमें से प्रत्येक का व्यास 50 cm है, जैसा कि आकृति में दर्शाया गया है। फर्श के उस भाग का क्षेत्रफल ज्ञात कीजिए जिस पर टाइल नहीं लगी हैं (π = 3.14 का प्रयोग कीजिए)।

वृत्त की उस जीवा द्वारा निर्मित दोनों वृत्तखंडों के क्षेत्रफलों का अंतर ज्ञात कीजिए, जिसकी लंबाई 5 cm है और जो केंद्र पर 90∘ का कोण अंतरित करती है।
