Advertisements
Advertisements
प्रश्न
15 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 60° का कोण अंतरित करती है। वृत्त के संगत लघु और प्रमुख खण्डों के क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73`]
5 cm त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर 60° का कोण अंतरित करती है। संगत लघु और दीर्घ वृत्तखंडों के क्षेत्रफल ज्ञात कौजिए। [π = 3.14 और `sqrt3 = 1.73` का प्रयोग कीजिए।]
उत्तर
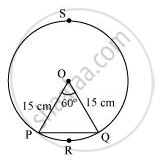
वृत्त की त्रिज्या (r) = 15 सेमी
त्रिज्यखंड OPRQ का क्षेत्रफल = `60^@/360^@xxpir^2`
= `1/6 xx 3.14 xx (15)^2`
= 117.75 सेमी2
ΔOPQ में,
∠OPQ = ∠OQP (As OP = OQ)
∠OPQ + ∠OQP + ∠POQ = 180°
2 ∠OPQ = 120°
∠OPQ = 60°
ΔOPQ एक समबाहु त्रिभुज है।
∠OPQ का क्षेत्रफल = `(sqrt3)/4 xx (r)^2`
= `sqrt3/4 xx (15)^2`
= `(225sqrt3)/4 "सेमी"^2`
= `56.25sqrt3`
97.3125 सेमी2
खंड PRQ का क्षेत्रफल = त्रिज्यखंड ΔPRQ का क्षेत्रफल − OPQ का क्षेत्रफल
= 117.75 − 97.3125
= 20.4375 सेमी2
वृहत खंड PSQ का क्षेत्रफल = वृत्त का क्षेत्रफल − खंड PRQ का क्षेत्रफल
= πr2 − 20.4375
= π × (15)2 − 20.4375
= 3.14 × 225 − 20.4375
= 706.5 − 20.4375
= 686.0625 सेमी2
APPEARS IN
संबंधित प्रश्न
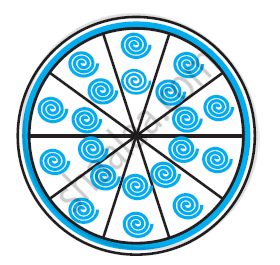
एक वृत्ताकार ब्रूच को चाँदी के तार से बनाया जाना है जिसका व्यास 35 मिमी है। तार को वृत्त के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्यखंडों में विभाजित करता है जैसा कि आकृति में दर्शाया गया है। तो ज्ञात कीजिए:
- कुल वांछित चाँदी के तार की लंबाई
- ब्रूच के प्रत्येक त्रिज्यखंड का क्षेत्रफल [उपयोग π = `22/7`]
एक छतरी में आठ ताने हैं, जो बराबर दूरी पर लगे हुए हैं। छतरी को 45 सेमी त्रिज्या वाला एक सपाट वृत्त मानते हुए, इसकी दो क्रमागत तानों के बीच का क्षेत्रफल ज्ञात कीजिए।
व्यासों 36 cm और 20 cm वाले दो वृत्तों की परिधियों के योग के बराबर परिधि वाले एक वृत्त की त्रिज्या ______ है।
दो भिन्न वृत्तों के दो त्रिज्यखंडों के क्षेत्रफल बराबर हैं। क्या यह आवश्यक है कि इन त्रिज्यखंडों के संगत चापों की लंबाइयाँ बराबर होंगी? क्यों?
दो वृत्तों के क्षेत्रफल बराबर हैं। क्या यह आवश्यक है कि इन वृत्तों की परिधियाँ भी बराबर हों? क्यों?
विमाओं 20 m × 16 m वाले एक आयताकार खेत के कोने पर एक गाय 14 m लंबी रस्सी से बँधी हुई है। खेत का वह क्षेत्रफल ज्ञात कीजिए जिसमें गाय चर सकती है।
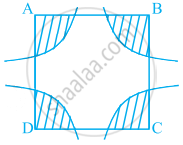
आकृति में, चतुर्भुज ABCD के A, B, C और D शीर्षों को केंद्र मानकर और 21 cm की त्रिज्या लेकर चाप खींचें गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
किसी वृत्त के 200° केंद्रीय कोण वाले एक त्रिज्यखंड का क्षेत्रफल 770 cm2 है। इस त्रिज्यखंड के संगत चाप की लंबाई ज्ञात कीजिए।
त्रिज्याओं 7 cm और 21 cm वाले दो वृत्तों के दो त्रिज्यखंडों के केंद्रीय कोण क्रमशः 120∘ और 40∘ हैं। इन दोनों त्रिज्यखंडों के क्षेत्रफल तथा साथ ही संगत चापों की लंबाई ज्ञात कीजिए। आप क्या देखते हैं?
10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
संगत दीर्घ त्रिज्यखंड [प्रयोग कीजिए = 3.14]
