Advertisements
Advertisements
Question
आकृति में, दिये छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।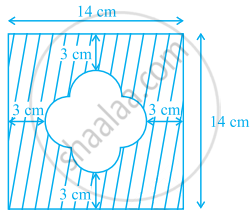
Solution
ABCD 14 सेमी भुजा वाला एक वर्ग है।
JK, KL, LM और MJ से जुड़ें।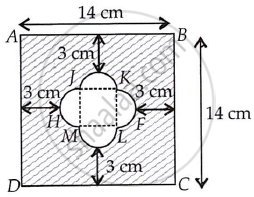
चार समान अर्ध-वृत्त हैं और JKLM ने एक वर्ग बनाया है।
∴ FH = 14 – (3 + 3) = 8 cm
तो, वर्ग JKLM की भुजा 4 cm है और दोनों सिरों के अर्ध-वृत्त की त्रिज्या 2 cm है।
∴ वर्ग JKLM का क्षेत्रफल = (4)2 = 16 cm2
अर्ध-वृत्त HJM का क्षेत्रफल = `(π"r"^2)/2`
= `(π xx (2)^2)/2`
= 2π cm2
∴ चार अर्ध-वृत्तों का क्षेत्रफल
= 4 × 2π
= 8π cm2
अब, वर्ग ABCD का क्षेत्रफल = (14)2 cm2 = 196 cm2
∴ छायांकित क्षेत्र का क्षेत्रफल = वर्ग का क्षेत्रफल
ABCD – [चार अर्ध-वृत्तों का क्षेत्रफल + वर्ग JKLM का क्षेत्रफल]
= 196 – [8π + 16]
= 196 – 16 – 8π
= (180 – 8π) cm2
अतः, छायांकित क्षेत्र का आवश्यक क्षेत्रफल (180 – 8π) cm2 है।
APPEARS IN
RELATED QUESTIONS
एक वृत्त, के चतुर्थांश का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22 सेमी है। `[pi = 22/7 "का प्रयोग करें"]`
12 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 120° का कोण अंतरित करती है। वृत्त के संगत वृत्त खण्ड का क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73 ` का प्रयोग कीजिए।]
दो वृत्तों के क्षेत्रफल बराबर हैं। क्या यह आवश्यक है कि इन वृत्तों की परिधियाँ भी बराबर हों? क्यों?
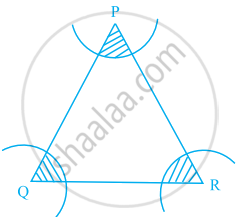
आकृति में, 14 cm की त्रिज्याएँ लेकर तथा P, Q और R को केंद्र मान कर चाप खींचे गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
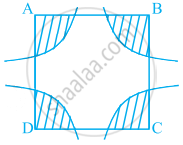
आकृति में, चतुर्भुज ABCD के A, B, C और D शीर्षों को केंद्र मानकर और 21 cm की त्रिज्या लेकर चाप खींचें गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
एक 20 cm लंबे तार के टुकड़े को मोड़कर एक वृत्त का चाप बनाया गया है, जो इस वृत्त के केंद्र पर 60° का कोण अंतरित करता है। वृत्त की त्रिज्या ज्ञात कीजिए।
त्रिज्या 12 cm वाले वृत्त के उस वृत्तखंड का क्षेत्रफल ज्ञात कीजिए, जिसके संगत त्रिज्यखंड का केंद्रीय कोण 60° है (π=3.14 का प्रयोग कीजिए)।
बराबर त्रिज्या 7 cm त्रिज्या वाले चार वृत्ताकार गत्ते के टुकड़ों को एक कागज पर इस प्रकार रखा गया है कि प्रत्येक टुकड़ा अन्य दो टुकड़ों को स्पर्श करता है। इन टुकड़ों के बीच में परिबद्ध भाग का क्षेत्रफल ज्ञात कीजिए।
किसी कमरे के फर्श की विमाएँ 5 m × 4 m हैं और इस पर वृत्ताकार टाइलें लगायी जाती हैं, जिनमें से प्रत्येक का व्यास 50 cm है, जैसा कि आकृति में दर्शाया गया है। फर्श के उस भाग का क्षेत्रफल ज्ञात कीजिए जिस पर टाइल नहीं लगी हैं (π = 3.14 का प्रयोग कीजिए)।

