Advertisements
Advertisements
प्रश्न
आकृति में, ABCD एक समलंब है, जिसमें AB || DC, AB = 18 cm, DC = 32 cm तथा AB और DC के बीच की दूरी = 14 cm है। यदि A, B, C और D को केंद्र मानकर त्रिज्याओं 7 cm के चाप खींचे गये हैं, तो इस आकृति के छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
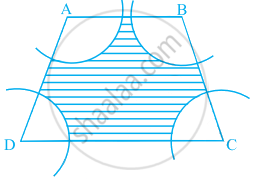
उत्तर
AB = 18 cm,
DC = 32 cm
AB और DC के बीच की दूरी = ऊँचाई = 14 cm
अब, समलंब का क्षेत्रफल
= `1/2 xx "समानांतर भुजाओं का योग" xx "ऊँचाई"`
= `1/2 xx 18 + 32 xx 14`
= 350 cm2
AB || DC के रूप में,
∴ ∠A + ∠D = 180°
और ∠B + ∠C = 180°
साथ ही, प्रत्येक चाप की त्रिज्या = 7 cm
इसलिए,
केंद्रीय कोण A वाले त्रिज्यखंड का क्षेत्रफल = `1/2 xx (∠"A")/180^circ xx π xx "r"^2`
केंद्रीय कोण D वाले त्रिज्यखंड का क्षेत्रफल = `1/2 xx (∠"D")/180^circ xx π xx "r"^2`
केंद्रीय कोण B वाले त्रिज्यखंड का क्षेत्रफल = `1/2 xx (∠"B")/180^circ xx π xx "r"^2`
केंद्रीय कोण C वाले त्रिज्यखंड का क्षेत्रफल = `1/2 xx (∠"C")/180^circ xx π xx "r"^2`
सेक्टरों का कुल क्षेत्रफल,
= `(∠"A")/360^circ xx pi xx "r"^2 + (∠"D")/360^circ xx pi xx "r"^2 + (∠"B")/360^circ xx pi xx "r"^2 + (∠"C")/360^circ xx pi xx "r"^2`
= `((∠"A" + ∠"D")/360^circ xx pi xx "r"^2) + ((∠"B" + ∠"C")/360^circ xx pi xx "r"^2)`
= `(180^circ/360^circ xx 22/7 xx 49) + (180^circ/360^circ xx 22/7 xx 49)`
= 77 + 77
= 154
∴ छायांकित क्षेत्र का क्षेत्रफल
= समलंब का क्षेत्रफल – (सेक्टरों का कुल क्षेत्रफल)
= 350 – 154
= 196 cm2
अतः, छायांकित क्षेत्र का आवश्यक क्षेत्रफल 196 सेमी2 है।
APPEARS IN
संबंधित प्रश्न
एक वृत्त, के चतुर्थांश का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22 सेमी है। `[pi = 22/7 "का प्रयोग करें"]`
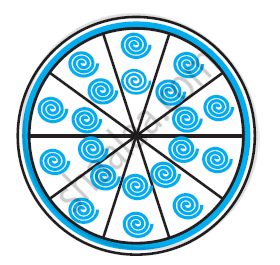
एक वृत्ताकार ब्रूच को चाँदी के तार से बनाया जाना है जिसका व्यास 35 मिमी है। तार को वृत्त के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्यखंडों में विभाजित करता है जैसा कि आकृति में दर्शाया गया है। तो ज्ञात कीजिए:
- कुल वांछित चाँदी के तार की लंबाई
- ब्रूच के प्रत्येक त्रिज्यखंड का क्षेत्रफल [उपयोग π = `22/7`]
एक मोटर साइकिल के पहिये की त्रिज्या 35 cm है। 66 km/h की चाल रखने के लिए, पहिये को प्रति मिनट कितने चक्कर लगाने चाहिए?
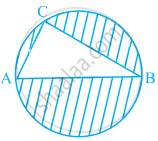
आकृति में, AB वृत का व्यास है, AC = 6 cm और BC = 8 cm है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए (π = 3.14 का प्रयोग कीजिए)।
त्रिज्या 5 cm वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए जिसके संगत चाप की लंबाई 3.5 cm है।
बराबर त्रिज्या 7 cm त्रिज्या वाले चार वृत्ताकार गत्ते के टुकड़ों को एक कागज पर इस प्रकार रखा गया है कि प्रत्येक टुकड़ा अन्य दो टुकड़ों को स्पर्श करता है। इन टुकड़ों के बीच में परिबद्ध भाग का क्षेत्रफल ज्ञात कीजिए।
त्रिज्याओं 7 cm और 21 cm वाले दो वृत्तों के दो त्रिज्यखंडों के केंद्रीय कोण क्रमशः 120∘ और 40∘ हैं। इन दोनों त्रिज्यखंडों के क्षेत्रफल तथा साथ ही संगत चापों की लंबाई ज्ञात कीजिए। आप क्या देखते हैं?
वृत्त की उस जीवा द्वारा निर्मित दोनों वृत्तखंडों के क्षेत्रफलों का अंतर ज्ञात कीजिए, जिसकी लंबाई 5 cm है और जो केंद्र पर 90∘ का कोण अंतरित करती है।
