Advertisements
Advertisements
प्रश्न
उत्तर
माना कि एक वृत्ताकार पहिये द्वारा लगाए गए चक्करों की संख्या n है और वृत्ताकार पहिये की त्रिज्या r है।
दिया गया है कि, वृत्ताकार पहिये का क्षेत्रफल = 1.54 m2 है।
⇒ πr2 = 1.54 ...[∵ वृत्ताकार πr2 का क्षेत्रफल]
⇒ r2 = `1.54/22 xx 7`
⇒ r2 = 0.49
∴ r = 0.7 m
तो, पहिये की त्रिज्या 0.7 m है।
एक वृत्ताकार पहिये द्वारा एक चक्कर में तय की गई दूरी = वृत्ताकार पहिये की परिधि
= 2πr
= `2 xx 22/7 xx 0.7`
= `22/5`
= 4.4 m ...[∵ वृत्त की परिधि = 2πr]
चूँकि, एक वृत्ताकार पहिये द्वारा तय की गई दूरी = 176 m है।
∴ चक्करों की संख्या = `"कुल दूरी"/"एक चक्कर में दूरी"`
= `176/4.4`
= 40
अतः, एक वृत्ताकार पहिये द्वारा बनाए गए चक्करों की आवश्यक संख्या 40 है।
APPEARS IN
संबंधित प्रश्न
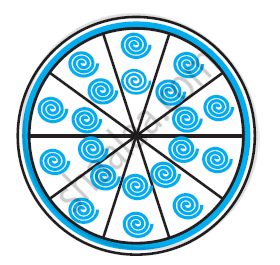
एक वृत्ताकार ब्रूच को चाँदी के तार से बनाया जाना है जिसका व्यास 35 मिमी है। तार को वृत्त के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्यखंडों में विभाजित करता है जैसा कि आकृति में दर्शाया गया है। तो ज्ञात कीजिए:
- कुल वांछित चाँदी के तार की लंबाई
- ब्रूच के प्रत्येक त्रिज्यखंड का क्षेत्रफल [उपयोग π = `22/7`]
यदि R1 और R2 त्रिज्याओं वाले दो वृत्तों की परिधियों का योग त्रिज्या R वाले एक वृत्त की परिधि के बराबर हो, तो ______।
दो भिन्न वृत्तों के दो त्रिज्यखंडों के क्षेत्रफल बराबर हैं। क्या यह आवश्यक है कि इन त्रिज्यखंडों के संगत चापों की लंबाइयाँ बराबर होंगी? क्यों?
विमाओं 20 m × 16 m वाले एक आयताकार खेत के कोने पर एक गाय 14 m लंबी रस्सी से बँधी हुई है। खेत का वह क्षेत्रफल ज्ञात कीजिए जिसमें गाय चर सकती है।
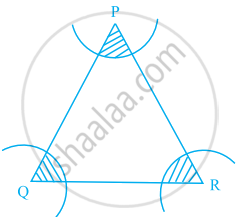
आकृति में, 14 cm की त्रिज्याएँ लेकर तथा P, Q और R को केंद्र मान कर चाप खींचे गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
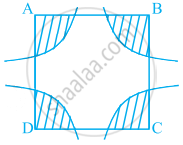
आकृति में, चतुर्भुज ABCD के A, B, C और D शीर्षों को केंद्र मानकर और 21 cm की त्रिज्या लेकर चाप खींचें गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
एक 20 cm लंबे तार के टुकड़े को मोड़कर एक वृत्त का चाप बनाया गया है, जो इस वृत्त के केंद्र पर 60° का कोण अंतरित करता है। वृत्त की त्रिज्या ज्ञात कीजिए।
बराबर त्रिज्या 7 cm त्रिज्या वाले चार वृत्ताकार गत्ते के टुकड़ों को एक कागज पर इस प्रकार रखा गया है कि प्रत्येक टुकड़ा अन्य दो टुकड़ों को स्पर्श करता है। इन टुकड़ों के बीच में परिबद्ध भाग का क्षेत्रफल ज्ञात कीजिए।
किसी वृत्त के 200° केंद्रीय कोण वाले एक त्रिज्यखंड का क्षेत्रफल 770 cm2 है। इस त्रिज्यखंड के संगत चाप की लंबाई ज्ञात कीजिए।
10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
संगत दीर्घ त्रिज्यखंड [प्रयोग कीजिए = 3.14]
