Advertisements
Advertisements
प्रश्न
एक वृत्ताकार मेजपोश, जिसकी त्रिज्या 32 सेमी है, में बीच में एक समबाहु ABC त्रिभुज छोड़ते हुए एक डिजाइनर बना हुआ है, जैसा कि आकृति में दिखाया गया है। इस छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = 22/7]
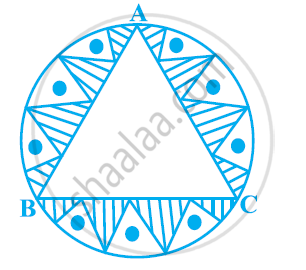
उत्तर
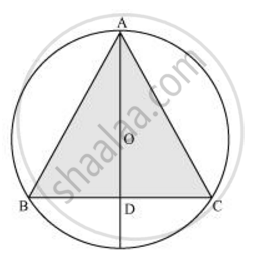
वृत्त की त्रिज्या (r) = 32 cm
AD ΔABC की माध्यिका है।
`AO =2/3 AD = 32`
AD = 48 सेमी
ΔABD में,
AB2 = AD2 + BD2
`AB^2 = (48)^2 + ((AB)/2)^2`
`(3AB^2)/4 = (48)^2`
`AB = (48xx2)/sqrt3 = 96/sqrt3`
`= 32sqrt3 "सेमी"`
समबाहु त्रिभुज का क्षेत्रफल ΔABC = `sqrt3/4(32sqrt3)^2`
`=sqrt3/4 xx 32xx32xx2 = 96xx8xxsqrt3`
`= 768sqrt3 "सेमी"^2`
वृत्त का क्षेत्रफल = r2
`= 22/7xx(32)^2`
`=22/7 xx 1024`
`= 22528/7 "सेमी"^2`
डिजाइन का क्षेत्रफल = वृत्त का क्षेत्रफल - ABC का क्षेत्रफल
`= ((22528)/7 - 768sqrt3) "सेमी"^2`
APPEARS IN
संबंधित प्रश्न
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि ABCD भुजा 14 सेमी का एक वर्ग है तथा APD और BPC दो अर्धवृत्त हैं। [उपयोग Π = `22/7`]
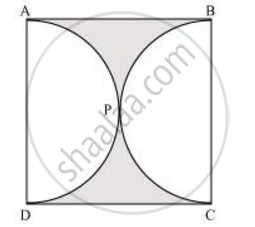
यदि R1 और R2 त्रिज्याओं वाले दो वृत्तों की परिधियों का योग त्रिज्या R वाले एक वृत्त की परिधि के बराबर हो, तो ______।
क्या यह कहना सत्य है कि व्यास d cm वाले एक वृत्ताकार पहिए द्वारा एक परिभ्रमण में चली गयी दूरी 2 π d cm होती है? क्यों?
दो भिन्न वृत्तों के दो त्रिज्यखंडों के क्षेत्रफल बराबर हैं। क्या यह आवश्यक है कि इन त्रिज्यखंडों के संगत चापों की लंबाइयाँ बराबर होंगी? क्यों?
आकृति में, AB वृत का व्यास है, AC = 6 cm और BC = 8 cm है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए (π = 3.14 का प्रयोग कीजिए)।
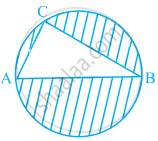
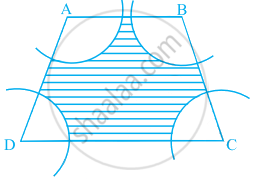
आकृति में, ABCD एक समलंब है, जिसमें AB || DC, AB = 18 cm, DC = 32 cm तथा AB और DC के बीच की दूरी = 14 cm है। यदि A, B, C और D को केंद्र मानकर त्रिज्याओं 7 cm के चाप खींचे गये हैं, तो इस आकृति के छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
किसी धनुर्विद्या (या तीरंदाजी) लक्ष्य के तीन क्षेत्र हैं, जो आकृति में दर्शाए अनुसार तीन संकेंद्रीय वृत्तों से बने हैं। यदि इन संकेंद्रीय वृत्तों के व्यास 1 : 2 : 3 के अनुपात में हैं, तो इन तीनों क्षेत्रों के क्षेत्रफलों का अनुपात ज्ञात कीजिए।

त्रिज्या 21 cm वाले एक वृत्त के 120∘ कोण वाले त्रिज्यखंड और उसके संगत दीर्घ त्रिज्यखंड के क्षेत्रफलों का अंतर ज्ञात कीजिए।
त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए।
चाप द्वारा बनाए गए त्रिज्यखंड का क्षेत्रफल [प्रयोग कीजिए =`22/7`]
