Advertisements
Advertisements
प्रश्न
भुजा 4 सेमी वाले एक वर्ग के प्रत्येक कोने से 1 सेमी त्रिज्या वाले वृत्त का एक चतुर्थांश काटा गया है तथा बीच में 2 सेमी व्यास का एक वृत भी काटा गया है, जैसा कि आकृति में दर्शाया गया है। वर्ग के शेष भाग का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = `22/7`]

उत्तर
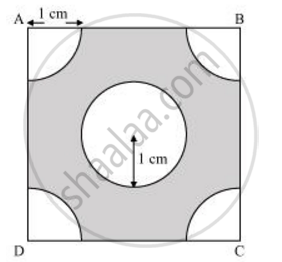
प्रत्येक चतुर्थांश 1 सेमी त्रिज्या वाले वृत्त में 90° का त्रिज्यखंड है।
प्रत्येक चतुर्थांश का क्षेत्रफल = `90^@/360^@pir^2`
`= 1/4xx22/7xx(1)^2 = 22/28 "सेमी"^2`
वर्ग का क्षेत्रफल = (भुजा)2 = (4)2 = 16 सेमी2
वृत्त का क्षेत्रफल = r2 = (1)2
`= 22/7 "सेमी"^2`
छायांकित क्षेत्र का क्षेत्रफल = वर्ग का क्षेत्रफल - वृत्त का क्षेत्रफल - 4 × चतुर्थांश का क्षेत्रफल
` = 16 -22/7 - 4 xx 22/28`
`= 16-22/7-22/7 = 16 - 44/7`
`= (112-44)/7 = 68/7 "सेमी"^2`
APPEARS IN
संबंधित प्रश्न
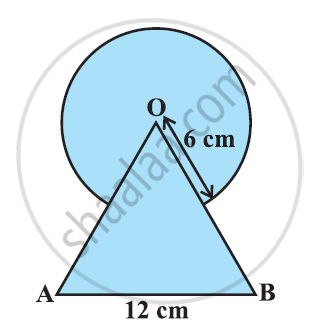
दी गई आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, जहाँ भुजा 12 सेमी वाले एक समबाहु त्रिभुज OAB के शीर्ष O को केंद्र मान कर 6 सेमी त्रिज्या वाला एक वृत्तीय चाप खींचा गया है। [उपयोग Π = `22/7`]
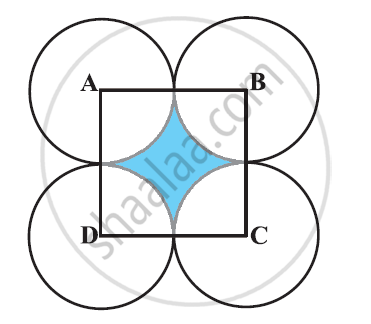
दी गई आकृति में, ABCD भुजा 14 सेमी वाला एक वर्ग है। A, B, C और D को केंद्र मानकर, चार वृत्त इस प्रकार खींचे गए हैं कि प्रत्येक वृत्त तीन शेष वृत्तों में दो वृत्तों को बाह्य रूप से स्पर्श करता है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = 22/7]
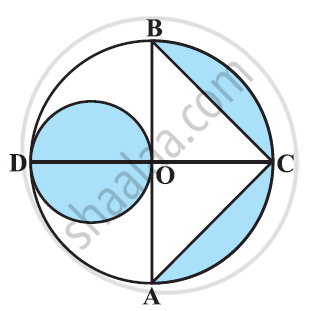
दी गई आकृति में AB और CD केंद्र O वाले एक वृत्त के दो परस्पर लंब व्यास हैं तथा OD छोटे वृत्त का व्यास है। यदि OA = 7 सेमी है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = `22/7`]
दी गई आकृति में OACB केंद्र O और त्रिज्या 3.5 सेमी वाले एक वृत्त का चतुर्थांस है। यदि OD = 2 सेमी है, तो निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
- चतुर्थांस OACB
- छायांकित भाग
[उपयोग Π = `22/7`]

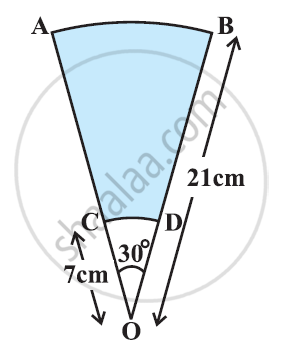
AB और CD केंद्र O तथा त्रिज्याओं 21 सेमी और 7 सेमी वाले दो सकेंद्रीय वृत्तों के क्रमश: दो चाप हैं। यदि ∠AOB = 30° तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
[उपयोग Π = `22/7`]
दी गई आकृति में, ABC त्रिज्या 12 सेमी वाले एक वृत का चतुर्थांश है तथा BC को व्यास मानकर एक अर्धवृत्त्त खींचा गया है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = 22/7]

दी गई आकृति में छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए, जो 8 सेमी त्रिज्याओं वाले दो वृत्तों के चतुर्थांशों के बीच उभयनिष्ठ है। [उपयोग Π = 22/7]

त्रिज्या 8 cm वाले एक वृत्त के अंतर्गत खींचे जा सकने वाले वर्ग का क्षेत्रफल ______ है।
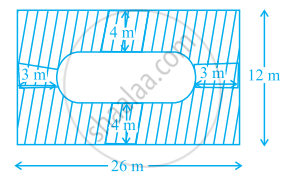
आकृति में दर्शायी गयी फूलों की क्यारी (अर्धवृत्ताकार सिरों वाली) का क्षेत्रफल ज्ञात कीजिए।
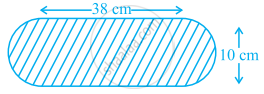
आकुति में, छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।