Advertisements
Advertisements
प्रश्न
एक वृत्ताकार मेजपोश, जिसकी त्रिज्या 32 सेमी है, में बीच में एक समबाहु ABC त्रिभुज छोड़ते हुए एक डिजाइनर बना हुआ है, जैसा कि आकृति में दिखाया गया है। इस छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = 22/7]
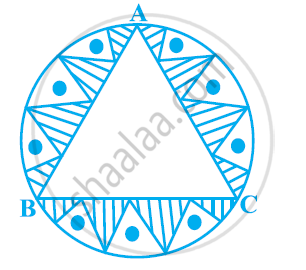
उत्तर
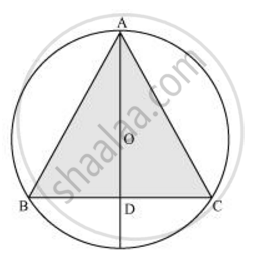
वृत्त की त्रिज्या (r) = 32 cm
AD ΔABC की माध्यिका है।
`AO =2/3 AD = 32`
AD = 48 सेमी
ΔABD में,
AB2 = AD2 + BD2
`AB^2 = (48)^2 + ((AB)/2)^2`
`(3AB^2)/4 = (48)^2`
`AB = (48xx2)/sqrt3 = 96/sqrt3`
`= 32sqrt3 "सेमी"`
समबाहु त्रिभुज का क्षेत्रफल ΔABC = `sqrt3/4(32sqrt3)^2`
`=sqrt3/4 xx 32xx32xx2 = 96xx8xxsqrt3`
`= 768sqrt3 "सेमी"^2`
वृत्त का क्षेत्रफल = r2
`= 22/7xx(32)^2`
`=22/7 xx 1024`
`= 22528/7 "सेमी"^2`
डिजाइन का क्षेत्रफल = वृत्त का क्षेत्रफल - ABC का क्षेत्रफल
`= ((22528)/7 - 768sqrt3) "सेमी"^2`
APPEARS IN
संबंधित प्रश्न
6 सेमी त्रिज्या वाले एक वृत्त के एक त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 60 डिग्री है। `[pi = 22/7 "का प्रयोग करें"]`
15 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 60° का कोण अंतरित करती है। वृत्त के संगत लघु और प्रमुख खण्डों के क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73`]
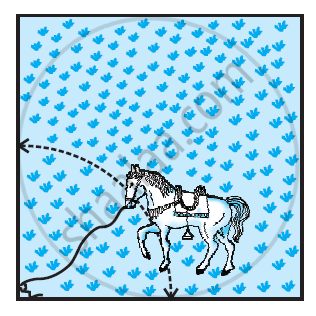
15 m भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूँटे से एक घोड़े को 5 m लंबी रस्सी से बाँध दिया गया है। ज्ञात कीजिए:
- मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
- चरे जा सकने वाले क्षेत्रफल में वृद्धि, यदि घोड़े को 5 m लंबी रस्सी के स्थान पर 10 m लंबी रस्सी से बाँध दिया जाए। [उपयोग = 3.14]
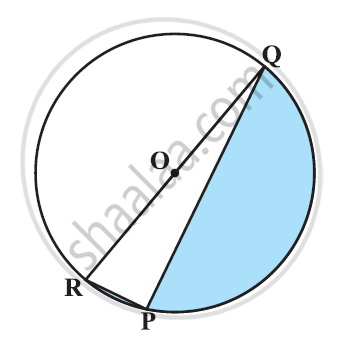
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि PQ = 24 सेमी, PR = 7 सेमी तथा O वृत्त का केंद्र है। [उपयोग Π = `22/7`]
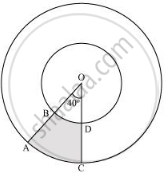
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि केंद्र O वाले दोनों सकेंद्रीय वृत्तों की त्रिज्याएँ क्रमश: 7 सेमी और 14 सेमी हैं तथा ∠AOC=40° है।
[Use Π = `22/7`]
आकृति में, व्यास d वाले एक वृत्त के अंतर्गत एक वर्ग खींचा गया है तथा एक अन्य वर्ग इसी वृत्त के परिगत है। क्या बाहरी वर्ग का क्षेत्रफल आंतरिक वर्ग के क्षेत्रफल का चार गुना है? अपने उत्तर का कारण दीजिए।

s मीटर की दूरी चलने के लिए, त्रिज्या r मीटर वाला एक वृत्ताकार पहिया `s/(2πr)` चक्कर लगाता है। क्या यह कथन सत्य है? क्यों?
विमाओं 20 m × 16 m वाले एक आयताकार खेत के कोने पर एक गाय 14 m लंबी रस्सी से बँधी हुई है। खेत का वह क्षेत्रफल ज्ञात कीजिए जिसमें गाय चर सकती है।
किसी वृत्ताकार खेल के मैदान का क्षेत्रफल 22176 m2 है। इस मैदान पर 50 रु प्रति मीटर की दर से बाड़ लगवाने का व्यय ज्ञात कीजिए।
त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए।
चाप द्वारा बनाए गए त्रिज्यखंड का क्षेत्रफल [प्रयोग कीजिए =`22/7`]
