Advertisements
Advertisements
प्रश्न
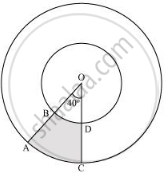
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि केंद्र O वाले दोनों सकेंद्रीय वृत्तों की त्रिज्याएँ क्रमश: 7 सेमी और 14 सेमी हैं तथा ∠AOC=40° है।
[Use Π = `22/7`]
उत्तर
भीतरी वृत्त की त्रिज्या = 7 सेमी
बाहरी वृत्त की त्रिज्या = 14 सेमी
छायांकित क्षेत्र का क्षेत्रफल = त्रिज्यखंड OAFC का क्षेत्रफल - त्रिज्यखंड OBED का क्षेत्रफल
`= 40^@/360^@ xx pi(14)^2 - 40^@/360^@ xx pi(7)^2`
`= 1/9xx22/7xx14xx14-1/9xx22/7xx7xx7`
`= 616/9-154/9=462/9`
`= 154/3 "सेमी"^2`
APPEARS IN
संबंधित प्रश्न
एक घड़ी की मिनट की सुई की लंबाई 14 सेमी है। इस सुई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए। `[pi = 22/7 "का प्रयोग करें"]`
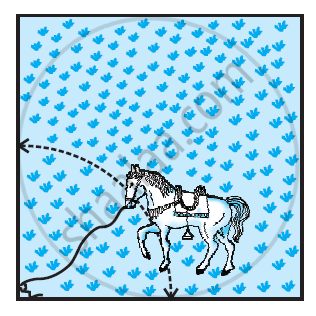
15 m भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूँटे से एक घोड़े को 5 m लंबी रस्सी से बाँध दिया गया है। ज्ञात कीजिए:
- मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
- चरे जा सकने वाले क्षेत्रफल में वृद्धि, यदि घोड़े को 5 m लंबी रस्सी के स्थान पर 10 m लंबी रस्सी से बाँध दिया जाए। [उपयोग = 3.14]
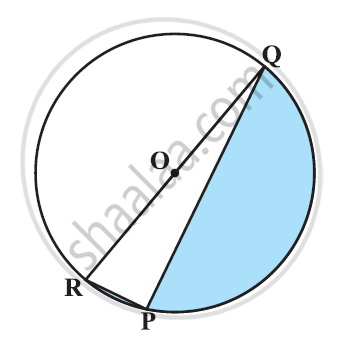
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि PQ = 24 सेमी, PR = 7 सेमी तथा O वृत्त का केंद्र है। [उपयोग Π = `22/7`]
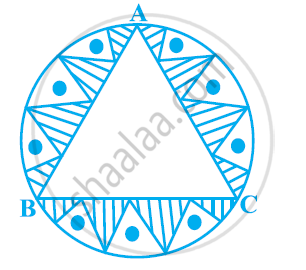
एक वृत्ताकार मेजपोश, जिसकी त्रिज्या 32 सेमी है, में बीच में एक समबाहु ABC त्रिभुज छोड़ते हुए एक डिजाइनर बना हुआ है, जैसा कि आकृति में दिखाया गया है। इस छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = 22/7]
क्या यह कहना सत्य है कि एक वृत्तखंड का क्षेत्रफल संगत त्रिज्यखंड के क्षेत्रफल से कम होता है? क्यों?
s मीटर की दूरी चलने के लिए, त्रिज्या r मीटर वाला एक वृत्ताकार पहिया `s/(2πr)` चक्कर लगाता है। क्या यह कथन सत्य है? क्यों?
यदि त्रिज्या r वाले एक वृत्त के एक चाप की लंबाई त्रिज्या 2r वाले एक वृत्त के चाप की लंबाई के बराबर हो, तो पहले वृत्त के संगत त्रिज्यखंड का कोण दूसरे वृत्त के संगत त्रिज्यखंड के कोण का दोग़ना होता है? क्या यह कथन असत्य है? क्यों?
दो वृत्तों के क्षेत्रफल बराबर हैं। क्या यह आवश्यक है कि इन वृत्तों की परिधियाँ भी बराबर हों? क्यों?
किसी ट्रैक्टर के अगले और पिछले पहियों के व्यास क्रमशः 80 cm और 2m हैं। ज्ञात कीजिए कि पिछले पहिए द्वारा उतनी दूरी तय करने में कितने चक्कर लगाने होंगे, जितनी दूरी अगला पहिया 1400 चक्कर लगाने पर तय करता है।
एक समचतुर्भुज के सभी शीर्ष एक वृत्त पर स्थित हैं। इस समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए, यदि वृत्त का क्षेत्रफल 1256 cm2 है (π = 3.14 का प्रयोग कीजिए)।
