Advertisements
Advertisements
प्रश्न
एक समचतुर्भुज के सभी शीर्ष एक वृत्त पर स्थित हैं। इस समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए, यदि वृत्त का क्षेत्रफल 1256 cm2 है (π = 3.14 का प्रयोग कीजिए)।
उत्तर
दिया गया है कि वृत्त का क्षेत्रफल 1256 cm2 है।
πr2 = 12563.14 × r2
3.14 × r2 = 1256
r2 = `1256/3.14`
r2 = 400
r = 20 cm
यदि एक समचतुर्भुज के सभी शीर्ष एक वृत्त पर स्थित हों, तो समचतुर्भुज वर्गाकार होता है।
निम्नलिखित चित्र पर विचार करें।
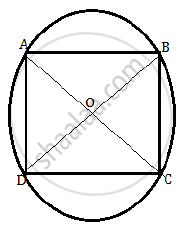
यहां A, B, C और D वृत्त पर चार बिंदु हैं।
इस प्रकार, OA = OB = OC = OD = वृत्त की त्रिज्या।
⇒ AC और BD वृत्त के व्यास हैं।
ΔADC पर विचार करें।
पाइथागोरस प्रमेय द्वारा, हमारे पास है,
AD2 + CD2 = AC2
2AD2 = (2 × 20)2 ...[AD = CD]
2AD2 = (40)2
AD2 = `1600/2`
AD2 = 800 cm2
यदि AD वर्ग की भुजा है, तो AD2 वर्ग का क्षेत्रफल है।
इस प्रकार वर्ग का क्षेत्रफल 800 cm2 है।
APPEARS IN
संबंधित प्रश्न
एक घड़ी की मिनट की सुई की लंबाई 14 सेमी है। इस सुई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए। `[pi = 22/7 "का प्रयोग करें"]`
15 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 60° का कोण अंतरित करती है। वृत्त के संगत लघु और प्रमुख खण्डों के क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73`]
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि ABCD भुजा 14 सेमी का एक वर्ग है तथा APD और BPC दो अर्धवृत्त हैं। [उपयोग Π = `22/7`]
दो वृत्तों के क्षेत्रफल बराबर हैं। क्या यह आवश्यक है कि इन वृत्तों की परिधियाँ भी बराबर हों? क्यों?
विमाओं 20 m × 16 m वाले एक आयताकार खेत के कोने पर एक गाय 14 m लंबी रस्सी से बँधी हुई है। खेत का वह क्षेत्रफल ज्ञात कीजिए जिसमें गाय चर सकती है।
आकृति में, चतुर्भुज ABCD के A, B, C और D शीर्षों को केंद्र मानकर और 21 cm की त्रिज्या लेकर चाप खींचें गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
किसी वृत्ताकार खेल के मैदान का क्षेत्रफल 22176 m2 है। इस मैदान पर 50 रु प्रति मीटर की दर से बाड़ लगवाने का व्यय ज्ञात कीजिए।
एक त्रिभुजाकार खेत की भुजाएँ 15 m, 16 m और 17 m हैं। इस खेत में चरने के लिए, इसके तीनों कोनों से एक गाय, एक भैंस और एक घोड़े को अलग-अलग 7 m लंबी रस्सियों से बाँध दिया गया है। खेत के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें ये तीनों पशु चर नहीं पाएँगे।
त्रिज्या 12 cm वाले वृत्त के उस वृत्तखंड का क्षेत्रफल ज्ञात कीजिए, जिसके संगत त्रिज्यखंड का केंद्रीय कोण 60° है (π=3.14 का प्रयोग कीजिए)।
त्रिज्याओं 7 cm और 21 cm वाले दो वृत्तों के दो त्रिज्यखंडों के केंद्रीय कोण क्रमशः 120∘ और 40∘ हैं। इन दोनों त्रिज्यखंडों के क्षेत्रफल तथा साथ ही संगत चापों की लंबाई ज्ञात कीजिए। आप क्या देखते हैं?
