Advertisements
Advertisements
प्रश्न
एक समचतुर्भुज के सभी शीर्ष एक वृत्त पर स्थित हैं। इस समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए, यदि वृत्त का क्षेत्रफल 1256 cm2 है (π = 3.14 का प्रयोग कीजिए)।
उत्तर
दिया गया है कि वृत्त का क्षेत्रफल 1256 cm2 है।
πr2 = 12563.14 × r2
3.14 × r2 = 1256
r2 = `1256/3.14`
r2 = 400
r = 20 cm
यदि एक समचतुर्भुज के सभी शीर्ष एक वृत्त पर स्थित हों, तो समचतुर्भुज वर्गाकार होता है।
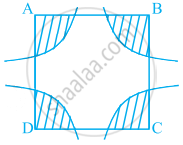
निम्नलिखित चित्र पर विचार करें।
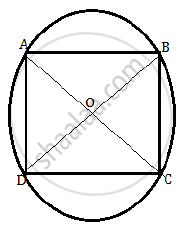
यहां A, B, C और D वृत्त पर चार बिंदु हैं।
इस प्रकार, OA = OB = OC = OD = वृत्त की त्रिज्या।
⇒ AC और BD वृत्त के व्यास हैं।
ΔADC पर विचार करें।
पाइथागोरस प्रमेय द्वारा, हमारे पास है,
AD2 + CD2 = AC2
2AD2 = (2 × 20)2 ...[AD = CD]
2AD2 = (40)2
AD2 = `1600/2`
AD2 = 800 cm2
यदि AD वर्ग की भुजा है, तो AD2 वर्ग का क्षेत्रफल है।
इस प्रकार वर्ग का क्षेत्रफल 800 cm2 है।
APPEARS IN
संबंधित प्रश्न
10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
संगत लघु वृत्तखंड [प्रयोग कीजिए π = 3.14]
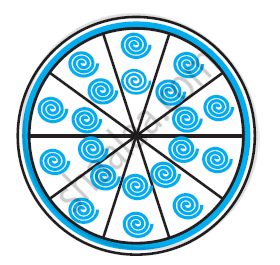
एक वृत्ताकार ब्रूच को चाँदी के तार से बनाया जाना है जिसका व्यास 35 मिमी है। तार को वृत्त के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्यखंडों में विभाजित करता है जैसा कि आकृति में दर्शाया गया है। तो ज्ञात कीजिए:
- कुल वांछित चाँदी के तार की लंबाई
- ब्रूच के प्रत्येक त्रिज्यखंड का क्षेत्रफल [उपयोग π = `22/7`]
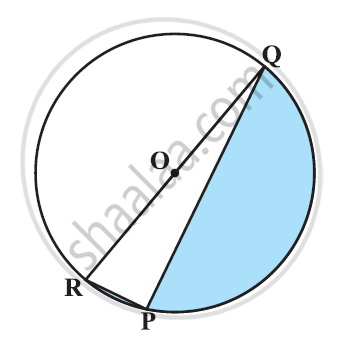
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि PQ = 24 सेमी, PR = 7 सेमी तथा O वृत्त का केंद्र है। [उपयोग Π = `22/7`]
आकृति में, व्यास d वाले एक वृत्त के अंतर्गत एक वर्ग खींचा गया है तथा एक अन्य वर्ग इसी वृत्त के परिगत है। क्या बाहरी वर्ग का क्षेत्रफल आंतरिक वर्ग के क्षेत्रफल का चार गुना है? अपने उत्तर का कारण दीजिए।

s मीटर की दूरी चलने के लिए, त्रिज्या r मीटर वाला एक वृत्ताकार पहिया `s/(2πr)` चक्कर लगाता है। क्या यह कथन सत्य है? क्यों?
दो भिन्न वृत्तों के बराबर लंबाइयों वाले चापों के संगत त्रिज्यखंडों के क्षेत्रफल बराबर होते हैं। क्या यह कथन सत्य है? क्यों?
उस वृत्त की त्रिज्या ज्ञात कीजिए, जिसकी परिधि त्रिज्याओं 15 cm और 18 cm वाले दो वृत्तों की परिधियों के योग के बराबर है।
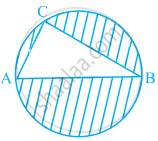
आकृति में, AB वृत का व्यास है, AC = 6 cm और BC = 8 cm है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए (π = 3.14 का प्रयोग कीजिए)।
आकृति में, चतुर्भुज ABCD के A, B, C और D शीर्षों को केंद्र मानकर और 21 cm की त्रिज्या लेकर चाप खींचें गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
बराबर त्रिज्या 7 cm त्रिज्या वाले चार वृत्ताकार गत्ते के टुकड़ों को एक कागज पर इस प्रकार रखा गया है कि प्रत्येक टुकड़ा अन्य दो टुकड़ों को स्पर्श करता है। इन टुकड़ों के बीच में परिबद्ध भाग का क्षेत्रफल ज्ञात कीजिए।
