Advertisements
Advertisements
प्रश्न
त्रिज्याओं 7 cm और 21 cm वाले दो वृत्तों के दो त्रिज्यखंडों के केंद्रीय कोण क्रमशः 120∘ और 40∘ हैं। इन दोनों त्रिज्यखंडों के क्षेत्रफल तथा साथ ही संगत चापों की लंबाई ज्ञात कीजिए। आप क्या देखते हैं?
उत्तर
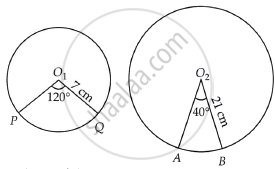
मान लीजिए कि संगत चापों की लंबाई l1 और l2 है।
दिया गया है कि, त्रिज्यखण्ड PO1QP की त्रिज्या = 7 cm
और त्रिज्यखण्ड AO2BA की त्रिज्या = 21 cm
त्रिज्यखंड PO1QP (θ1) का केंद्रीय कोण = 120°
और त्रिज्यखंड AO2BA (θ2) का केंद्रीय कोण = 40°
∴ केंद्रीय कोण O1 वाले त्रिज्यखंड का क्षेत्रफल
= `(pi"r"^2)/360^circ xx θ_1`
= `(pi(7)^2)/360^circ xx 120^circ`
= `22/7 xx (7 xx 7)/360^circ xx 120^circ`
= `(22 xx 7)/3`
= `154/3 "cm"^2`
और केंद्रीय कोण O2 वाले त्रिज्यखंड का क्षेत्रफल
= `(pi"r"^2)/360^circ xx θ_2`
= `(pi(21)^2)/360^circ xx 40^circ`
= `22/7 xx (21 xx 21)/360^circ xx 40^circ`
= `(22 xx 3 xx 21)/9`
= 22 × 7
= 154 cm2
अब, त्रिज्यखंड PO1QP की संगत चाप लंबाई
= `θ_1/360^circ xx 2pi"r"`
= `120^circ/360^circ xx 2 xx 22/7 xx 7`
= `44/3 "cm"`
और सेक्टर AO2BA की संगत चाप लंबाई
= `θ_2/360^circ xx 2pi"r"`
= `40^circ/360^circ xx 2 xx 22/7 xx 21`
= `44/3 "cm"`
इसलिए, हम देखते हैं कि दो अलग-अलग वृत्तों के दो त्रिज्यखंडों की चाप की लंबाई समान हो सकती है लेकिन उनका क्षेत्रफल समान होना आवश्यक नहीं है।
APPEARS IN
संबंधित प्रश्न
12 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 120° का कोण अंतरित करती है। वृत्त के संगत वृत्त खण्ड का क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73 ` का प्रयोग कीजिए।]
दो भिन्न वृत्तों के बराबर लंबाइयों वाले चापों के संगत त्रिज्यखंडों के क्षेत्रफल बराबर होते हैं। क्या यह कथन सत्य है? क्यों?
विमाओं 20 m × 16 m वाले एक आयताकार खेत के कोने पर एक गाय 14 m लंबी रस्सी से बँधी हुई है। खेत का वह क्षेत्रफल ज्ञात कीजिए जिसमें गाय चर सकती है।
त्रिज्या 14 cm वाले एक वृत्त के लघु वृत्तखंड का क्षेत्रफल ज्ञात कीजिए, जिसके संगत त्रिज्यखंड का कोण 60° है।
एक 20 cm लंबे तार के टुकड़े को मोड़कर एक वृत्त का चाप बनाया गया है, जो इस वृत्त के केंद्र पर 60° का कोण अंतरित करता है। वृत्त की त्रिज्या ज्ञात कीजिए।
बराबर त्रिज्या 3.5 cm वाले तीन वृत्त इस प्रकार खींचे गये हैं कि इनमें से प्रत्येक अन्य दो वृत्तों को स्पर्श करता है। इन वृत्तों से परिबद्ध क्षेत्रफल ज्ञात कीजिए।
एक समचतुर्भुज के सभी शीर्ष एक वृत्त पर स्थित हैं। इस समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए, यदि वृत्त का क्षेत्रफल 1256 cm2 है (π = 3.14 का प्रयोग कीजिए)।
त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए।
चाप द्वारा बनाए गए त्रिज्यखंड का क्षेत्रफल [प्रयोग कीजिए =`22/7`]
