Advertisements
Advertisements
प्रश्न
Answer the following question.
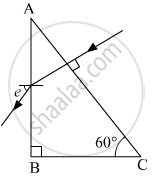
Calculate the angle of emergence (e) of the ray of light incident normally on the face AC of a glass prism ABC of refractive index `sqrt(3)`. How will the angle of emergence change qualitatively, if the ray of light emerges from the prism into a liquid of refractive index 1.3 instead of air?
उत्तर
Snell's law says `mu_1 Sin("i") = mu_2 Sin("r")`
`mu_"Prism" = sqrt(3)`
`mu_"Prism" = (30°) = sin (e)`
`sqrt(3) xx 1/2 = sin (e)`
`e = 60°`
Now when the external medium is changed to liquid of `mu_"L" = 1.3 "then",`
`mu_"prism" Sin (30) = mu_"L" sin (e)`
`sqrt(3) Sin (30°) = 1.3 Sin (e)`
`"e" = Sin^-1 (sqrt(3)/(2xx1.3)) = 41.83°`
Hence the angle of emergence reduces to 41.83° from 60°.
APPEARS IN
संबंधित प्रश्न
Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.
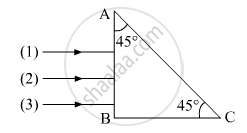
Three rays (1, 2, 3) of different colours fall normally on one of the sides of an isosceles right angled prism as shown. The refractive index of prism for these rays is 1.39, 1.47 and 1.52 respectively. Find which of these rays get internally reflected and which get only refracted from AC. Trace the paths of rays. Justify your answer with the help of necessary calculations.
A ray of light, incident on an equilateral prism `(μ_g = sqrt3)`moves parallel to the base line of the prism inside it. Find the angle of incidence for this ray.
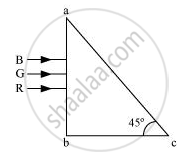
Three light rays red (R), green (G) and blue (B) are incident on a right angled prism ‘abc’ at face ‘ab’. The refractive indices of the material of the prism for red, green and blue wavelengths are 1.39, 1.44 and 1.47 respectively. Out of the three which colour ray will emerge out of face ‘ac’? Justify your answer. Trace the path of these rays after passing through face ‘ab’.
Suggest a method to produce a rainbow in your house.
For a glass prism `(µ = sqrt(3))` the angle of minimum deviation is equal to the angle of the prism. Find the angle of the prism.
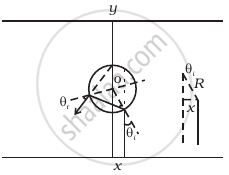
An infinitely long cylinder of radius R is made of an unusual exotic material with refractive index –1 (Figure). The cylinder is placed between two planes whose normals are along the y direction. The center of the cylinder O lies along the y-axis. A narrow laser beam is directed along the y direction from the lower plate. The laser source is at a horizontal distance x from the diameter in the y direction. Find the range of x such that light emitted from the lower plane does not reach the upper plane.
The maximum value of the index of refraction of a material of a prism which allows the passage of light through it when the refracting angle of the prism is A is ______.
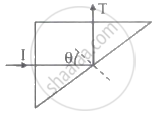
A triangular prism of glass is shown in the figure. A ray incident normally to one face is totally internally reflected. If θ is 45°, then the index of refraction of the glass is ______.
Two concave refracting surfaces of equal radii of curvature face each other in the air as shown in the figure. The point object O is placed midway between the centre and one of the poles. Then the separation between the images of O formed by each refracting surface is ______.