Advertisements
Advertisements
प्रश्न
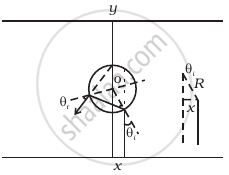
An infinitely long cylinder of radius R is made of an unusual exotic material with refractive index –1 (Figure). The cylinder is placed between two planes whose normals are along the y direction. The center of the cylinder O lies along the y-axis. A narrow laser beam is directed along the y direction from the lower plate. The laser source is at a horizontal distance x from the diameter in the y direction. Find the range of x such that light emitted from the lower plane does not reach the upper plane.
उत्तर
Here the material has refractive index – 1, θr is negative and `θ_r^'` positive.
Now, `|θ_i| = |θ_r| = |θ_r^'|`
The total deviation of the outcoming ray from the incoming ray is 4θt. Rays shall not reach the receiving plate if `pi/4 ≤ 4θ_i ≤ (3pi)/2` [angles measured clockwise from the yiaxis]
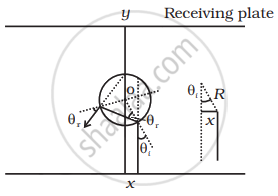
On solving, `pi/8 ≤ θ_i ≤ (3pi)/8`
Now, `sin θ_i = x/R`
`pi/8 ≤ sin^-1 x/R ≤ (3pi)/8` or `pi/8 ≤ x/R ≤ (3pi)/8`
Thus for light emitted from the source shall not reach the receiving plane if `(Rpi)/2 ≤ x ≤ (3Rpi)/8`.
APPEARS IN
संबंधित प्रश्न
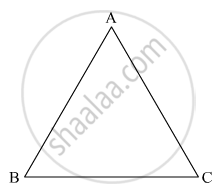
Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.
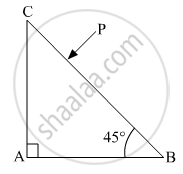
Trace the path of the ray (P) of light passing through the glass prism as shown in the figure. The prism is made of glass with critical angle ic = 41°.
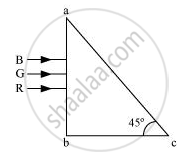
Three light rays red (R), green (G) and blue (B) are incident on a right angled prism ‘abc’ at face ‘ab’. The refractive indices of the material of the prism for red, green and blue wavelengths are 1.39, 1.44 and 1.47 respectively. Out of the three which colour ray will emerge out of face ‘ac’? Justify your answer. Trace the path of these rays after passing through face ‘ab’.
Can you ever have a situation in which a light ray goes undeviated through a prism?
Suggest a method to produce a rainbow in your house.
A small object is embedded in a glass sphere (μ = 1.5) of radius 5.0 cm at a distance 1.5 cm left to the centre. Locate the image of the object as seen by an observer standing (a) to the left of the sphere and (b) to the right of the sphere.
Answer the following question.
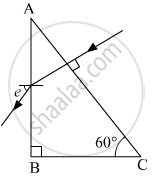
Calculate the angle of emergence (e) of the ray of light incident normally on the face AC of a glass prism ABC of refractive index `sqrt(3)`. How will the angle of emergence change qualitatively, if the ray of light emerges from the prism into a liquid of refractive index 1.3 instead of air?
A prism is made of glass of unknown refractive index. A parallel beam of light is incident on the face of the prism. The angle of minimum deviation is measured to be 40°. What is the refractive index of the material of the prism? The refracting angle of the prism is 60°. If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light.
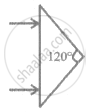
An isosceles prism of angle 120° has a refractive index 1.44. Two parallel monochromatic rays enter the prism parallel to each other in air as shown. The rays emerge from the opposite faces:
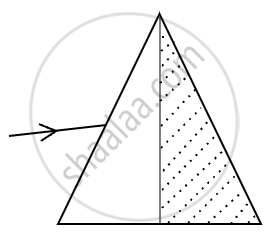
A ray of light when incident upon a thin prism suffers a minimum deviation of 39°. If the shaded half portion of the prism is removed, then the same ray will ______.