Question

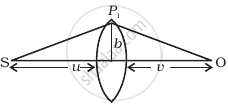
(i) Consider a thin lens placed between a source (S) and an observer (O) (Figure). Let the thickness of the lens vary as `w(b) = w_0 - b^2/α`, where b is the verticle distance from the pole. `w_0` is a constant. Using Fermat’s principle i.e. the time of transit for a ray between the source and observer is an extremum, find the condition that all paraxial rays starting from the source will converge at a point O on the axis. Find the focal length.

(ii) A gravitational lens may be assumed to have a varying width of the form

`w(b) = k_1ln(k_2/b) b_("min") < b < b_("max")`

= `k_1ln (K_2/b_("min")) b < b_("min")`

Show that an observer will see an image of a point object as a ring about the center of the lens with an angular radius

`β = sqrt((n - 1)k_1 u/v)/(u + v)`

Answer 1

(i) The time required to travel from S to P₁ is `t_1 = (SP_1)/c = sqrt(u^2 + b^2)/c ≃ u/c (1 + 1/2 b^2/u^2)` assuming b << u₀

The time required to travel from P₁ to O is `t_2 = (P_1O)/c = sqrt(v^2 + b^2)/c ≃ v/c(1 + 1/2 b^2/v^2)`

The time required to travel through the lens is `t_1 = ((n - 1)w(b))/c` where n is the refractive index.

Thus the total time is `t = 1/c[u + v + 1/2 b^2 (1/u + 1/v) + (n - 1)w(b)]`

Put `1/D = 1/u + 1/v`

Then `t = 1/c(u + v + 1/2 b^2/D + (n - 1)(w_0 + b^2/α))`

Fermet’s principle gives 

`(dt)/(db) = 0 = b/(CD) - (2(n - 1)b)/(cα)`

α = `2(n - 1)D`

Thus a convergent lens is formed if α = 2(n – 1)D. This is independent of b and hence all paraxial rays from S will converge at O (i.e. for rays b << n and b << v).

Since `1/D = 1/u + 1/v`, the focal length is D.

(ii) In this case

`t = 1/c(u + v + 1/2 b^2/D + (n - 1) k_1ln (k_2/b))`

`(dt)/(db) = 0 = b/D - (n - 1) k_1/b`

⇒ b² = `(n - 1) k_1D`

∴ b = `sqrt((n - 1)k_1D`

Thus all rays passing at a height b shall contribute to the image. The ray paths make an angle

`β ≃ b/v = sqrt((n - 1)k_1D)/v^2 = sqrt(((n - 1)k_1uv)/(v^2(u + v))) = sqrt(((n - 1)k_1u)/((u + v)v))`.