Advertisements
Advertisements
प्रश्न
The focal length of a convex lens made of glass of refractive index (1.5) is 20 cm.
What will be its new focal length when placed in a medium of refractive index 1.25?
Is focal length positive or negative? What does it signify?
उत्तर
Given aμg = 1.5
Focal length of the given convex lens when it is placed in air is f = + 20 cm
Refractive index of the given medium with respect to air is aμm = 1.25
New focal length of the given convex lens when placed in a medium is f'
`1/"f" = ("a"_(mu"g") - 1)[(1/"R"_1) + (1/"R"_2)]` .....(A)
`1/"f'" = ("m"_(mu"g") - 1)[(1/"R"_1) + (1/"R"_2)]` .....(B)
Dividing (A) by (B), we get
`"f'"/"f" = (("a"_(mu"g") - 1))/(("m"_(mu"g") - 1)) = ((1.5 - 1))/((1.2 - 1)) = 0.5/0.2 = 5/2 = 2.5`
f' = 2.5f = (2.5 × 20) cm = +50 cm as mµg = `mu_"g"/mu_"m" = 1.5/1.25 = 1.2`
New focal length is positive.
The significance of the positive sign of the focal length is that the given convex lens is still converging in the given medium.
APPEARS IN
संबंधित प्रश्न
A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of the image and the magnification. Describe what happens as the needle is moved farther from the mirror.
In motor vehicles, a convex mirror is attached near the driver's seat to give him the view of the traffic behind. What is the special function of this convex mirror which a plane mirror can not do?
A diverging lens of focal length 20 cm and a converging mirror of focal length 10 cm are placed coaxially at a separation of 5 cm. Where should an object be placed so that a real image is formed at the object itself?
A converging lens of focal length 12 cm and a diverging mirror of focal length 7.5 cm are placed 5.0 cm apart with their principal axes coinciding. Where should an object be placed so that its image falls on itself?
A converging lens and a diverging mirror are placed at a separation of 15 cm. The focal length of the lens is 25 cm and that of the mirror is 40 cm. Where should a point source be placed between the lens and the mirror so that the light, after getting reflected by the mirror and then getting transmitted by the lens, comes out parallel to the principal axis?
Consider the situation shown in figure. The elevator is going up with an acceleration of 2.00 m s−2 and the focal length of the mirror is 12.0 cm. All the surfaces are smooth and the pulley is light. The mass-pulley system is released from rest (with respect to the elevator) at t = 0 when the distance of B from the mirror is 42.0 cm. Find the distance between the image of the block B and the mirror at t = 0.200 s. Take g = 10 m s−2.
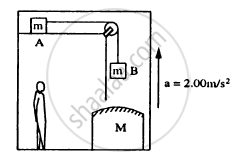
Answer the following question.
With the help of a ray diagram, obtain the relation between its focal length and radius of curvature.
According to Cartesian sign convention, all distances are measured from the _______.
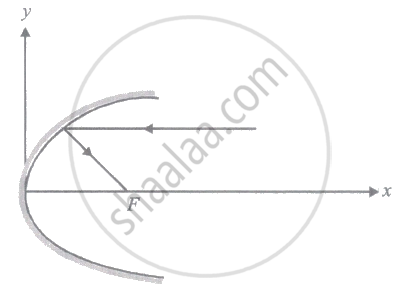
A parallel beam of light ray parallel to the x-axis is incident on a parabolic reflecting surface x = 2by2 as shown in the figure. After reflecting it passes through focal point F. What is the focal length of the reflecting surface?
The radius of curvature of the curved surface of a plano-convex lens is 20 cm. If the refractive index of the material of the lens be 1.5, it will ______.
