Advertisements
Advertisements
प्रश्न
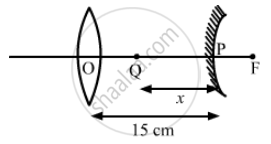
A converging lens and a diverging mirror are placed at a separation of 15 cm. The focal length of the lens is 25 cm and that of the mirror is 40 cm. Where should a point source be placed between the lens and the mirror so that the light, after getting reflected by the mirror and then getting transmitted by the lens, comes out parallel to the principal axis?
उत्तर
Given,
Distance between the convex lens and the convex mirror is 15 cm.
The focal length (f1) of the lens is 25 cm.
The focal length (f2) of the mirror is 40 cm.
Let x cm be the object distance from the mirror.
Therefore,
u = − x cm
v = 25 − 15 = + 10 cm (∵ focal length of lens = 25 cm)
∴ f1 = + 40 cm
Using lens formula:
\[\Rightarrow \frac{1}{v} + \frac{1}{u} = \frac{1}{f}\Rightarrow\frac{1}{x}=\frac{1}{10}-\frac{1}{40}\Rightarrow x=\frac{400}{30} = \frac{40}{3}\]
Thus, the object distance is \[\left( 15 - \frac{40}{3} \right)=\frac{5}{3}\]
= 1.67 cm from the lens
APPEARS IN
संबंधित प्रश्न
A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of the image and the magnification. Describe what happens as the needle is moved farther from the mirror.
A double convex lens is made of a glass of refractive index 1.55, with both faces of the same radius of curvature. Find the radius of curvature required, if the focal length is 20 cm.
Can mirrors give rise to chromatic aberration?
In image formation from spherical mirrors, only paraxial rays are considered because they
A spherical surface of radius 30 cm separates two transparent media A and B with refractive indices 1.33 and 1.48 respectively. The medium A is on the convex side of the surface. Where should a point object be placed in medium A so that the paraxial rays become parallel after refraction at the surface?
A narrow pencil of parallel light is incident normally on a solid transparent sphere of radius r. What should be the refractive index is the pencil is to be focussed (a) at the surface of the sphere, (b) at the centre of the sphere.
How can the spherical aberration produced by a lens be minimized?
Answer the following question.
Under what conditions is the phenomenon of total internal reflection of light observed? Obtain the relation between the critical angle of incidence and the refractive index of the medium.
Answer the following question.
Three lenses of focal length +10 cm, —10 cm and +30 cm are arranged coaxially as in the figure given below. Find the position of the final image formed by the combination.

Answer the following question.
With the help of a ray diagram, obtain the relation between its focal length and radius of curvature.
According to Cartesian sign convention, all distances are measured from the _______.
Focal length of a mirror is given by ______.
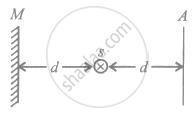
The intensity of a point source of light, S, placed at a distance d in front of a screen A, is I0 at the center of the screen. Find the light intensity at the center of the screen if a completely reflecting plane mirror M is placed at a distance d behind the source, as shown in the figure.
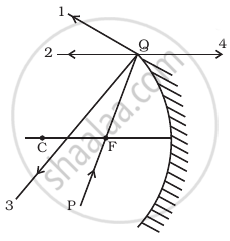
The direction of ray of light incident on a concave mirror is shown by PQ while directions in which the ray would travel after reflection is shown by four rays marked 1, 2, 3 and 4 (figure). Which of the four rays correctly shows the direction of reflected ray?
A car is moving with at a constant speed of 60 km h–1 on a straight road. Looking at the rear view mirror, the driver finds that the car following him is at a distance of 100 m and is approaching with a speed of 5 km h–1. In order to keep track of the car in the rear, the driver begins to glance alternatively at the rear and side mirror of his car after every 2 s till the other car overtakes. If the two cars were maintaining their speeds, which of the following statement (s) is/are correct?
An astronomical refractive telescope has an objective of focal length 20 m and an eyepiece of focal length 2 cm.
- The length of the telescope tube is 20.02 m.
- The magnification is 1000.
- The image formed is inverted.
- An objective of a larger aperture will increase the brightness and reduce chromatic aberration of the image.
(i) Consider a thin lens placed between a source (S) and an observer (O) (Figure). Let the thickness of the lens vary as `w(b) = w_0 - b^2/α`, where b is the verticle distance from the pole. `w_0` is a constant. Using Fermat’s principle i.e. the time of transit for a ray between the source and observer is an extremum, find the condition that all paraxial rays starting from the source will converge at a point O on the axis. Find the focal length.
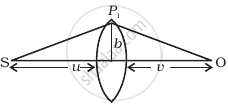
(ii) A gravitational lens may be assumed to have a varying width of the form
`w(b) = k_1ln(k_2/b) b_("min") < b < b_("max")`
= `k_1ln (K_2/b_("min")) b < b_("min")`
Show that an observer will see an image of a point object as a ring about the center of the lens with an angular radius
`β = sqrt((n - 1)k_1 u/v)/(u + v)`
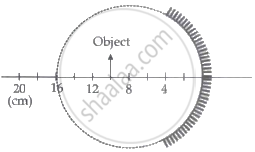
A spherical mirror is obtained as shown in the figure from a hollow glass sphere. if an object is positioned in front of the mirror, what will be the nature and magnification of the image of the object? (Figure drawn as schematic and not to scale)
If an object is placed at a distance of 10 cm in front of a concave mirror of a focal length of 20 cm, the image formed will be ______.
