Advertisements
Advertisements
प्रश्न
A double convex lens is made of a glass of refractive index 1.55, with both faces of the same radius of curvature. Find the radius of curvature required, if the focal length is 20 cm.
उत्तर
Refractive index of glass, μ=1.55
Focal length of the double-convex lens, f=20 cm
Radius of curvature of one face of the lens =R1
Radius of curvature of the other face of the lens =R2
Radius of curvature of the double-convex lens = R
∴ R1=R and R2=-R
The value of R can be calculated as:
`1/f=(mu-1)[1/R_1-1/R_2]`
`1/20=(1.55-1)[1/R+1/R]`
`1/20=(0.55)[2/R]`
`therefore R=22 cm`
Hence , the radius of curvature of the double-convex lens is 22 cm
संबंधित प्रश्न
The image of an extended object, placed perpendicular to the principal axis of a mirror, will be erect if
(a) the object and the image are both real
(b) the object and the image are both virtual
(c) the object is real but the image is virtual
(d) the object is virtual but the image is real.
Answer the following question.
Three lenses of focal length +10 cm, —10 cm and +30 cm are arranged coaxially as in the figure given below. Find the position of the final image formed by the combination.

Focal length of a mirror is given by ______.
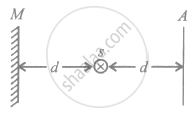
The intensity of a point source of light, S, placed at a distance d in front of a screen A, is I0 at the center of the screen. Find the light intensity at the center of the screen if a completely reflecting plane mirror M is placed at a distance d behind the source, as shown in the figure.
An astronomical refractive telescope has an objective of focal length 20 m and an eyepiece of focal length 2 cm.
- The length of the telescope tube is 20.02 m.
- The magnification is 1000.
- The image formed is inverted.
- An objective of a larger aperture will increase the brightness and reduce chromatic aberration of the image.
A short object of length L is placed along the principal axis of a concave mirror away from focus. The object distance is u. If the mirror has a focal length f, what will be the length of the image? You may take L << |v – f|.
(i) Consider a thin lens placed between a source (S) and an observer (O) (Figure). Let the thickness of the lens vary as `w(b) = w_0 - b^2/α`, where b is the verticle distance from the pole. `w_0` is a constant. Using Fermat’s principle i.e. the time of transit for a ray between the source and observer is an extremum, find the condition that all paraxial rays starting from the source will converge at a point O on the axis. Find the focal length.
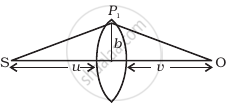
(ii) A gravitational lens may be assumed to have a varying width of the form
`w(b) = k_1ln(k_2/b) b_("min") < b < b_("max")`
= `k_1ln (K_2/b_("min")) b < b_("min")`
Show that an observer will see an image of a point object as a ring about the center of the lens with an angular radius
`β = sqrt((n - 1)k_1 u/v)/(u + v)`
A spherical mirror is obtained as shown in the figure from a hollow glass sphere. if an object is positioned in front of the mirror, what will be the nature and magnification of the image of the object? (Figure drawn as schematic and not to scale)
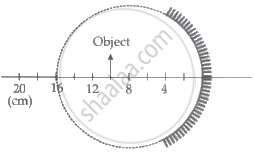
A concave mirror of focal length 12 cm forms three times the magnified virtual image of an object. Find the distance of the object from the mirror.
A converging lens has a focal length of 10 cm in air. It is made of a material with a refractive index of 1.6. If it is immersed in a liquid of refractive index 1.3, find its new focal length.
