Advertisements
Advertisements
प्रश्न
A short object of length L is placed along the principal axis of a concave mirror away from focus. The object distance is u. If the mirror has a focal length f, what will be the length of the image? You may take L << |v – f|.
उत्तर
As the mean distance of object from mirror is u
∴ `u_1 = u - L/2` and `u_2 = (u + L/2)`
Let the image of the two ends of object form at distance v1 and v2(v1 > v2). So length of image on principal axis is L' = (v1 – v2)
`1/v + 1/u = 1/f` or `1/v + 1/f = 1/u`
⇒ `1/v = (u - f)/(uf)`
⇒ `v = (uf)/(u - f)`
So L' = `v_1 - v_2 = ((u - L/2)f)/((u - L/2) - f) - ((u + L/2)f)/((u + L/2) - f)`
⇒ L' = `f (u - L/2)/((u - f - L/2)) - (u + 1/2)/((u - f + L/2))`
⇒ L' = `f[((u - L/2)(u - f + L/2) - (u + L/2)(u - f - L/2))/((u - f - L/2)(u - f + 1/2))]`
= `(f[u^2 - uf + (uL)/2 - (uL)/2 + (fL)/2 - L^2/4 - (u^2 - uf - (uL)/2 + (uL)/2 - (fL)/2 - L^2/4)])/((u - f)^2 - L^2/4)`
∴ `L < < (u - f)`
∴ `L^2/4 < < < (u - f)`
So neglecting the terms `L^2/4`
`L^2 = f[((fL)/2 + (fL)/2)/(u - f)^2]`
`L^2 = (ffL)/((u - f)^2` ⇒ `L^2 = (Lf^2)/((u - f)^2`
It is the length of image f.
APPEARS IN
संबंधित प्रश्न
If an object far away from a convex mirror moves towards the mirror, the image also moves. Does it move faster, slower or at the same speed as compared to the object?
In image formation from spherical mirrors, only paraxial rays are considered because they
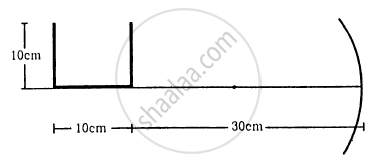
A U-shaped wire is placed before a concave mirror having radius of curvature 20 cm as shown in figure. Find the total length of the image.
A diverging lens of focal length 20 cm and a converging mirror of focal length 10 cm are placed coaxially at a separation of 5 cm. Where should an object be placed so that a real image is formed at the object itself?
Two thin lenses having optical powers of -10D and+ 6D are placed in contact with each other. The focal length of the combination is:
State how the focal length of a glass lens (Refractive Index 1.5) changes when it is completely immersed in:
(i) Water (Refractive Index 1.33)
(ii) A liquid (Refractive Index 1.65)
Answer the following question.
Under what conditions is the phenomenon of total internal reflection of light observed? Obtain the relation between the critical angle of incidence and the refractive index of the medium.
A thin converging lens of focal length 12 cm is kept in contact with a thin diverging lens of focal length 18 cm. Calculate the effective/equivalent focal length of the combination.
Why does a car driver use a convex mirror as a rear-view mirror?
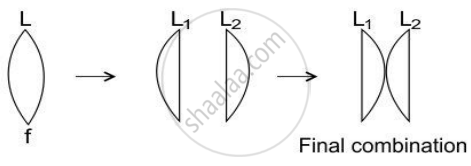
A lens of focal length f is divided into two equal parts and then these parts are put in a combination as shown in the figure below.
- What is the focal length of L1?
- What is the focal length of the final combination?