Advertisements
Advertisements
प्रश्न
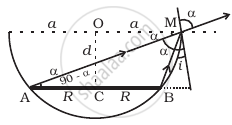
A circular disc of radius ‘R’ is placed co-axially and horizontally inside an opaque hemispherical bowl of radius ‘a’ (Figure). The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index µ and the near edge of the disc becomes just visible. How far below the top of the bowl is the disc placed?
उत्तर
In figure AM and BM are the rays from the ends of disc AB reaching at one end of bowl at M.MN is tangent at M, so MN ⊥ AB i.e., ∠N = 90°
Taking incidence ray BM and refracted ray MD
BN = CN – CB = OM – CB = a – R
MB = `sqrt(d^2 + (a - R^2))`
∴ `sin i = (BN)/(BM) = ((a - R))/sqrt(d^2 + (a - R)^2)`
∠r = ∠a = ∠AMN
`sin r = cos(90° - α) = (AN)/(AM) = (a + R)/sqrt(d^2 + (a + R)^2`
For incidence ray MN to the horizontal level of liquid MP, MN will be normal at M. ∠i and ∠r will be incidence and refracted angles when ray BM passes from liquid (μ) to air. By Snell's law, as ray passes from liquid to air
`1mu_0 = (sin i)/(sin r)` ⇒ `mu_0/mu_1 = (sin i )/(sin r)` .....[μ0 for air = 1] [μ1 for liquid]
`1/mu_0 = (sin i)/(sin r)`
`1/mu_1 = (sqrt(a - R)/sqrt(d^2 + (a - R)^2))/((a + R)/sqrt(d^2 + (a + R)^2)) = ((a - R) sqrt(d^2 + (a + R)^2))/((a + R)sqrt(a^2 + (a - R)^2)`
`d = (mu(a^2 - d^2))/(sqrt((a + r)^2 - mu(a - r)^2)`
It is required expression.
APPEARS IN
संबंधित प्रश्न
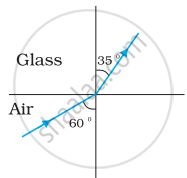
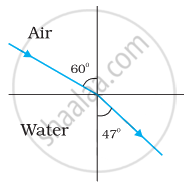
Figures (a) and (b) show the refraction of a ray in air incident at 60° with the normal to a glass-air and water-air interface, respectively. Predict the angle of refraction in the glass when the angle of incidence in water is 45° with the normal to a water-glass interface [Figure (c)].
 |
 |
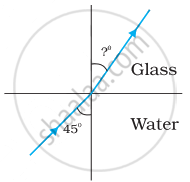 |
| (a) | (b) | (c) |
Does the apparent depth of a tank of water change if viewed obliquely? If so, does the apparent depth increase or decrease?
Determine the value of the angle of incidence for a ray of light travelling from a medium of refractive index \[\mu_1 = \sqrt{2}\] into the medium of refractive index \[\mu_2 = 1\] so that it just grazes along the surface of separation.
A laser light is focussed by a converging lens. Will there be a significant chromatic aberration?
A narrow beam of white light goes through a slab having parallel faces.
(a) The light never splits in different colours
(b) The emergent beam is white
(c) The light inside the slab is split into different colours
(d) The light inside the slab is white
A vessel contains water up to a height of 20 cm and above it an oil up to another 20 cm. The refractive indices of the water and the oil are 1.33 and 1.30 respectively. Find the apparent depth of the vessel when viewed from above.
Stars twinkle due to ______.
What is angle of deviation due to refraction?
What is looming?
The critical angle is maximum when light travels from ______.
`(a^mu"w"=4/3,a^mug=3/2)`
