Advertisements
Advertisements
प्रश्न
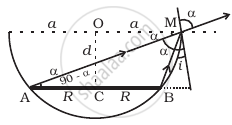
A circular disc of radius ‘R’ is placed co-axially and horizontally inside an opaque hemispherical bowl of radius ‘a’ (Figure). The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index µ and the near edge of the disc becomes just visible. How far below the top of the bowl is the disc placed?
उत्तर
In figure AM and BM are the rays from the ends of disc AB reaching at one end of bowl at M.MN is tangent at M, so MN ⊥ AB i.e., ∠N = 90°
Taking incidence ray BM and refracted ray MD
BN = CN – CB = OM – CB = a – R
MB = `sqrt(d^2 + (a - R^2))`
∴ `sin i = (BN)/(BM) = ((a - R))/sqrt(d^2 + (a - R)^2)`
∠r = ∠a = ∠AMN
`sin r = cos(90° - α) = (AN)/(AM) = (a + R)/sqrt(d^2 + (a + R)^2`
For incidence ray MN to the horizontal level of liquid MP, MN will be normal at M. ∠i and ∠r will be incidence and refracted angles when ray BM passes from liquid (μ) to air. By Snell's law, as ray passes from liquid to air
`1mu_0 = (sin i)/(sin r)` ⇒ `mu_0/mu_1 = (sin i )/(sin r)` .....[μ0 for air = 1] [μ1 for liquid]
`1/mu_0 = (sin i)/(sin r)`
`1/mu_1 = (sqrt(a - R)/sqrt(d^2 + (a - R)^2))/((a + R)/sqrt(d^2 + (a + R)^2)) = ((a - R) sqrt(d^2 + (a + R)^2))/((a + R)sqrt(a^2 + (a - R)^2)`
`d = (mu(a^2 - d^2))/(sqrt((a + r)^2 - mu(a - r)^2)`
It is required expression.
APPEARS IN
संबंधित प्रश्न
Double-convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length is to be 20 cm?
The refractive index of diamond is much greater than that of ordinary glass. Is this fact of some use to a diamond cutter?
A fish which is at a depth of l2 em .in water `(mu = 4/3)` is viewed by an observer on the bank of a lake. Its apparent depth as observed: by the observer is:
a) 3 cm
b) 9 cm
c) 12 cm
d) 16 cm
A laser light is focussed by a converging lens. Will there be a significant chromatic aberration?
A convex lens of focal length 20 cm and a concave lens of focal length 10 cm are placed 10 cm apart with their principal axes coinciding. A beam of light travelling parallel to the principal axis and having a beam diameter 5.0 mm, is incident on the combination. Show that the emergent beam is parallel to the incident one. Find the beam diameter of the emergent beam.
An object is immersed in a fluid of refractive index 'µ'. In order that the object becomes invisible when observed from outside, it should ______.
When a ray of light is incident normally on one refracting surface of an equilateral prism of refractive index 1.5, the emerging ray ______.
`[sin^-1(1/1.5)=41.8^circ]`
The optical density of turpentine is higher than that of water while its mass density is lower. Figure shows a layer of turpentine floating over water in a container. For which one of the four rays incident on turpentine in figure, the path shown is correct?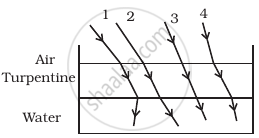
There are certain material developed in laboratories which have a negative refractive index (Figure). A ray incident from air (medium 1) into such a medium (medium 2) shall follow a path given by.
Three immiscible liquids of densities d1 > d2 > d3 and refractive indices µ1 > µ2 > µ3 are put in a beaker. The height of each liquid column is `h/3`. A dot is made at the bottom of the beaker. For near normal vision, find the apparent depth of the dot.
