Advertisements
Advertisements
Question
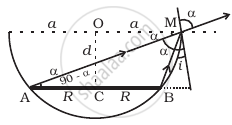
A circular disc of radius ‘R’ is placed co-axially and horizontally inside an opaque hemispherical bowl of radius ‘a’ (Figure). The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index µ and the near edge of the disc becomes just visible. How far below the top of the bowl is the disc placed?
Solution
In figure AM and BM are the rays from the ends of disc AB reaching at one end of bowl at M.MN is tangent at M, so MN ⊥ AB i.e., ∠N = 90°
Taking incidence ray BM and refracted ray MD
BN = CN – CB = OM – CB = a – R
MB = `sqrt(d^2 + (a - R^2))`
∴ `sin i = (BN)/(BM) = ((a - R))/sqrt(d^2 + (a - R)^2)`
∠r = ∠a = ∠AMN
`sin r = cos(90° - α) = (AN)/(AM) = (a + R)/sqrt(d^2 + (a + R)^2`
For incidence ray MN to the horizontal level of liquid MP, MN will be normal at M. ∠i and ∠r will be incidence and refracted angles when ray BM passes from liquid (μ) to air. By Snell's law, as ray passes from liquid to air
`1mu_0 = (sin i)/(sin r)` ⇒ `mu_0/mu_1 = (sin i )/(sin r)` .....[μ0 for air = 1] [μ1 for liquid]
`1/mu_0 = (sin i)/(sin r)`
`1/mu_1 = (sqrt(a - R)/sqrt(d^2 + (a - R)^2))/((a + R)/sqrt(d^2 + (a + R)^2)) = ((a - R) sqrt(d^2 + (a + R)^2))/((a + R)sqrt(a^2 + (a - R)^2)`
`d = (mu(a^2 - d^2))/(sqrt((a + r)^2 - mu(a - r)^2)`
It is required expression.
APPEARS IN
RELATED QUESTIONS
A tank is filled with water to a height of 12.5 cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be 9.4 cm. What is the refractive index of water? If water is replaced by a liquid of refractive index 1.63 up to the same height, by what distance would the microscope have to be moved to focus on the needle again?
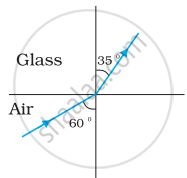
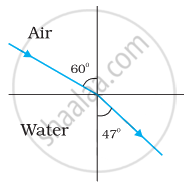
Figures (a) and (b) show the refraction of a ray in air incident at 60° with the normal to a glass-air and water-air interface, respectively. Predict the angle of refraction in the glass when the angle of incidence in water is 45° with the normal to a water-glass interface [Figure (c)].
 |
 |
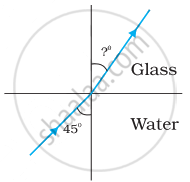 |
| (a) | (b) | (c) |
The refractive index of diamond is much greater than that of ordinary glass. Is this fact of some use to a diamond cutter?
A glass lens of refractive index 1.45 disappears when immersed in a liquid. What is the value of refractive index of the liquid?
If the light moving in a straight line bends by a small but fixed angle, it may be a case of
(a) reflection
(b) refraction
(c) diffraction
(d) dispersion.
A vessel contains water up to a height of 20 cm and above it an oil up to another 20 cm. The refractive indices of the water and the oil are 1.33 and 1.30 respectively. Find the apparent depth of the vessel when viewed from above.
What is optical path? Obtain the equation for optical path of a medium of thickness d and refractive index n.
Explain the reason for glittering of diamond.
What is looming?
A ray of light travels from air to water to glass and aga in from glass to air. Refractive index of water with respect to air is 'x' glass with respect to water is 'y' and air with respect to glass is 'z'. which one of the following is correct?
