Advertisements
Advertisements
प्रश्न
A short object of length L is placed along the principal axis of a concave mirror away from focus. The object distance is u. If the mirror has a focal length f, what will be the length of the image? You may take L << |v – f|.
Advertisements
उत्तर
As the mean distance of object from mirror is u
∴ `u_1 = u - L/2` and `u_2 = (u + L/2)`
Let the image of the two ends of object form at distance v1 and v2(v1 > v2). So length of image on principal axis is L' = (v1 – v2)
`1/v + 1/u = 1/f` or `1/v + 1/f = 1/u`
⇒ `1/v = (u - f)/(uf)`
⇒ `v = (uf)/(u - f)`
So L' = `v_1 - v_2 = ((u - L/2)f)/((u - L/2) - f) - ((u + L/2)f)/((u + L/2) - f)`
⇒ L' = `f (u - L/2)/((u - f - L/2)) - (u + 1/2)/((u - f + L/2))`
⇒ L' = `f[((u - L/2)(u - f + L/2) - (u + L/2)(u - f - L/2))/((u - f - L/2)(u - f + 1/2))]`
= `(f[u^2 - uf + (uL)/2 - (uL)/2 + (fL)/2 - L^2/4 - (u^2 - uf - (uL)/2 + (uL)/2 - (fL)/2 - L^2/4)])/((u - f)^2 - L^2/4)`
∴ `L < < (u - f)`
∴ `L^2/4 < < < (u - f)`
So neglecting the terms `L^2/4`
`L^2 = f[((fL)/2 + (fL)/2)/(u - f)^2]`
`L^2 = (ffL)/((u - f)^2` ⇒ `L^2 = (Lf^2)/((u - f)^2`
It is the length of image f.
APPEARS IN
संबंधित प्रश्न
A small candle, 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?
A double convex lens is made of a glass of refractive index 1.55, with both faces of the same radius of curvature. Find the radius of curvature required, if the focal length is 20 cm.
In image formation from spherical mirrors, only paraxial rays are considered because they
A U-shaped wire is placed before a concave mirror having radius of curvature 20 cm as shown in figure. Find the total length of the image.
A spherical surface of radius 30 cm separates two transparent media A and B with refractive indices 1.33 and 1.48 respectively. The medium A is on the convex side of the surface. Where should a point object be placed in medium A so that the paraxial rays become parallel after refraction at the surface?
Two thin lenses having optical powers of -10D and+ 6D are placed in contact with each other. The focal length of the combination is:
With the help of a ray diagram, obtain the relation between its focal length and radius of curvature.
Focal length of a mirror is given by ______.
A thin converging lens of focal length 12 cm is kept in contact with a thin diverging lens of focal length 18 cm. Calculate the effective/equivalent focal length of the combination.
The focal length of a convex lens made of glass of refractive index (1.5) is 20 cm.
What will be its new focal length when placed in a medium of refractive index 1.25?
Is focal length positive or negative? What does it signify?
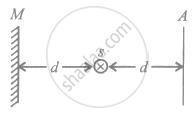
The intensity of a point source of light, S, placed at a distance d in front of a screen A, is I0 at the center of the screen. Find the light intensity at the center of the screen if a completely reflecting plane mirror M is placed at a distance d behind the source, as shown in the figure.
You are given four sources of light each one providing a light of a single colour – red, blue, green and yellow. Suppose the angle of refraction for a beam of yellow light corresponding to a particular angle of incidence at the interface of two media is 90°. Which of the following statements is correct if the source of yellow light is replaced with that of other lights without changing the angle of incidence?
A spherical mirror is obtained as shown in the figure from a hollow glass sphere. if an object is positioned in front of the mirror, what will be the nature and magnification of the image of the object? (Figure drawn as schematic and not to scale)
An object is 20 cm away from a concave mirror and it is within the focal length of the mirror. If the mirror is changed to a plane mirror, the image moves 15 cm closer to the mirror.
Focal length of the concave mirror is ______.
A particle is dropped along the axis from a height 15 cm on a concave mirror of focal length 30 cm as shown in figure. The acceleration due to gravity is 10 m/s2. Find the maximum speed of image in m/s:
A concave mirror of focal length 12 cm forms three times the magnified virtual image of an object. Find the distance of the object from the mirror.
A converging lens has a focal length of 10 cm in air. It is made of a material with a refractive index of 1.6. If it is immersed in a liquid of refractive index 1.3, find its new focal length.
