Advertisements
Advertisements
प्रश्न
A converging lens of focal length 40 cm is kept in contact with a diverging lens of focal length 30 cm. Find the focal length of the combination .
उत्तर
`1/(F') = 1/(f_1) + 1/(f_2) = 1/(+40) +1/(-30) =1/40 - 1/30`
`1/(F') = (3-47)/120 = 1/120 `cm [Diverging]
APPEARS IN
संबंधित प्रश्न
A small candle, 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?
In image formation from spherical mirrors, only paraxial rays are considered because they
A U-shaped wire is placed before a concave mirror having radius of curvature 20 cm as shown in figure. Find the total length of the image.
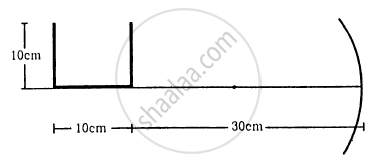
A converging lens and a diverging mirror are placed at a separation of 15 cm. The focal length of the lens is 25 cm and that of the mirror is 40 cm. Where should a point source be placed between the lens and the mirror so that the light, after getting reflected by the mirror and then getting transmitted by the lens, comes out parallel to the principal axis?
A short object of length L is placed along the principal axis of a concave mirror away from focus. The object distance is u. If the mirror has a focal length f, what will be the length of the image? You may take L << |v – f|.
A thin convex lens of focal length 25 cm is cut into two pieces 0.5 cm above the principal axis. The top part is placed at (0, 0) and an object placed at (– 50 cm, 0). Find the coordinates of the image.
(i) Consider a thin lens placed between a source (S) and an observer (O) (Figure). Let the thickness of the lens vary as `w(b) = w_0 - b^2/α`, where b is the verticle distance from the pole. `w_0` is a constant. Using Fermat’s principle i.e. the time of transit for a ray between the source and observer is an extremum, find the condition that all paraxial rays starting from the source will converge at a point O on the axis. Find the focal length.
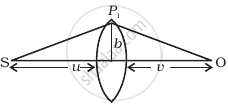
(ii) A gravitational lens may be assumed to have a varying width of the form
`w(b) = k_1ln(k_2/b) b_("min") < b < b_("max")`
= `k_1ln (K_2/b_("min")) b < b_("min")`
Show that an observer will see an image of a point object as a ring about the center of the lens with an angular radius
`β = sqrt((n - 1)k_1 u/v)/(u + v)`
Parallel rays striking a spherical mirror far from the optic axis are focussed at a different point than are rays near the axis thereby the focus moves toward the mirror as the parallel rays move toward the outer edge of the mirror. What value of incidence angle θ produces a 2% change in the location of the focus, compared to the location for θ very close to zero?
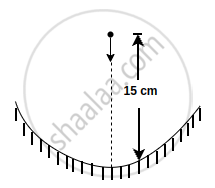
A particle is dropped along the axis from a height 15 cm on a concave mirror of focal length 30 cm as shown in figure. The acceleration due to gravity is 10 m/s2. Find the maximum speed of image in m/s:
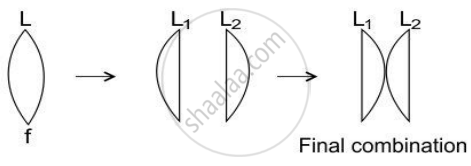
A lens of focal length f is divided into two equal parts and then these parts are put in a combination as shown in the figure below.
- What is the focal length of L1?
- What is the focal length of the final combination?