Advertisements
Advertisements
प्रश्न
A small candle, 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?
उत्तर
Size of the candle, h = 2.5 cm
Image size = h'
Object distance, u = −27 cm
Radius of curvature of the concave mirror, R = −36 cm
Focal length of the concave mirror, f = `"R"/2 = (-36)/2` = −18 cm
Image distance = v
The image distance can be obtained using the mirror formula:
`1/"u" + 1/"v" = 1/"f"`
`1/"v" = 1/"f" - 1/"u"`
= `1/-18 - 1/-27`
= `(-3 + 2)/54`
= `-1/54`
∴ v = −54 cm
Therefore, the screen should be placed 54 cm away from the mirror to obtain a sharp image.
The magnification of the image is given as:
`"m" = "h'"/"h" = - "v"/"u"`
∴ h' = `-"v"/"u" xx "h"`
= `-(-54)/(-27) xx 2.5`
= −5 cm
The height of the candle’s image is 5 cm. The negative sign indicates that the image is inverted and real.
If the candle is moved closer to the mirror, then the screen will have to be moved away from the mirror in order to obtain the image.
APPEARS IN
संबंधित प्रश्न
Can mirrors give rise to chromatic aberration?
In image formation from spherical mirrors, only paraxial rays are considered because they
Light is incident from glass (μ = 1.5) to air. Sketch the variation of the angle of deviation δ with the angle of incident i for 0 < i < 90°.
A narrow pencil of parallel light is incident normally on a solid transparent sphere of radius r. What should be the refractive index is the pencil is to be focussed (a) at the surface of the sphere, (b) at the centre of the sphere.
A converging lens of focal length 12 cm and a diverging mirror of focal length 7.5 cm are placed 5.0 cm apart with their principal axes coinciding. Where should an object be placed so that its image falls on itself?
A converging lens of focal length 40 cm is kept in contact with a diverging lens of focal length 30 cm. Find the focal length of the combination .
How can the spherical aberration produced by a lens be minimized?
State how the focal length of a glass lens (Refractive Index 1.5) changes when it is completely immersed in:
(i) Water (Refractive Index 1.33)
(ii) A liquid (Refractive Index 1.65)
Answer the following question.
With the help of a ray diagram, obtain the relation between its focal length and radius of curvature.
According to Cartesian sign convention, all distances are measured from the _______.
Focal length of a mirror is given by ______.
A thin converging lens of focal length 12 cm is kept in contact with a thin diverging lens of focal length 18 cm. Calculate the effective/equivalent focal length of the combination.
The radius of curvature of the curved surface of a plano-convex lens is 20 cm. If the refractive index of the material of the lens be 1.5, it will ______.
A short object of length L is placed along the principal axis of a concave mirror away from focus. The object distance is u. If the mirror has a focal length f, what will be the length of the image? You may take L << |v – f|.
A thin convex lens of focal length 25 cm is cut into two pieces 0.5 cm above the principal axis. The top part is placed at (0, 0) and an object placed at (– 50 cm, 0). Find the coordinates of the image.
(i) Consider a thin lens placed between a source (S) and an observer (O) (Figure). Let the thickness of the lens vary as `w(b) = w_0 - b^2/α`, where b is the verticle distance from the pole. `w_0` is a constant. Using Fermat’s principle i.e. the time of transit for a ray between the source and observer is an extremum, find the condition that all paraxial rays starting from the source will converge at a point O on the axis. Find the focal length.
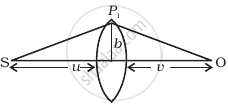
(ii) A gravitational lens may be assumed to have a varying width of the form
`w(b) = k_1ln(k_2/b) b_("min") < b < b_("max")`
= `k_1ln (K_2/b_("min")) b < b_("min")`
Show that an observer will see an image of a point object as a ring about the center of the lens with an angular radius
`β = sqrt((n - 1)k_1 u/v)/(u + v)`
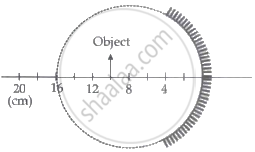
A spherical mirror is obtained as shown in the figure from a hollow glass sphere. if an object is positioned in front of the mirror, what will be the nature and magnification of the image of the object? (Figure drawn as schematic and not to scale)
Parallel rays striking a spherical mirror far from the optic axis are focussed at a different point than are rays near the axis thereby the focus moves toward the mirror as the parallel rays move toward the outer edge of the mirror. What value of incidence angle θ produces a 2% change in the location of the focus, compared to the location for θ very close to zero?
Why does a car driver use a convex mirror as a rear-view mirror?
