Advertisements
Advertisements
प्रश्न
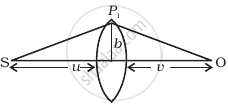
(i) Consider a thin lens placed between a source (S) and an observer (O) (Figure). Let the thickness of the lens vary as `w(b) = w_0 - b^2/α`, where b is the verticle distance from the pole. `w_0` is a constant. Using Fermat’s principle i.e. the time of transit for a ray between the source and observer is an extremum, find the condition that all paraxial rays starting from the source will converge at a point O on the axis. Find the focal length.
(ii) A gravitational lens may be assumed to have a varying width of the form
`w(b) = k_1ln(k_2/b) b_("min") < b < b_("max")`
= `k_1ln (K_2/b_("min")) b < b_("min")`
Show that an observer will see an image of a point object as a ring about the center of the lens with an angular radius
`β = sqrt((n - 1)k_1 u/v)/(u + v)`
उत्तर

(i) The time required to travel from S to P1 is `t_1 = (SP_1)/c = sqrt(u^2 + b^2)/c ≃ u/c (1 + 1/2 b^2/u^2)` assuming b << u0
The time required to travel from P1 to O is `t_2 = (P_1O)/c = sqrt(v^2 + b^2)/c ≃ v/c(1 + 1/2 b^2/v^2)`
The time required to travel through the lens is `t_1 = ((n - 1)w(b))/c` where n is the refractive index.
Thus the total time is `t = 1/c[u + v + 1/2 b^2 (1/u + 1/v) + (n - 1)w(b)]`
Put `1/D = 1/u + 1/v`
Then `t = 1/c(u + v + 1/2 b^2/D + (n - 1)(w_0 + b^2/α))`
Fermet’s principle gives
`(dt)/(db) = 0 = b/(CD) - (2(n - 1)b)/(cα)`
α = `2(n - 1)D`
Thus a convergent lens is formed if α = 2(n – 1)D. This is independent of b and hence all paraxial rays from S will converge at O (i.e. for rays b << n and b << v).
Since `1/D = 1/u + 1/v`, the focal length is D.
(ii) In this case
`t = 1/c(u + v + 1/2 b^2/D + (n - 1) k_1ln (k_2/b))`
`(dt)/(db) = 0 = b/D - (n - 1) k_1/b`
⇒ b2 = `(n - 1) k_1D`
∴ b = `sqrt((n - 1)k_1D`
Thus all rays passing at a height b shall contribute to the image. The ray paths make an angle
`β ≃ b/v = sqrt((n - 1)k_1D)/v^2 = sqrt(((n - 1)k_1uv)/(v^2(u + v))) = sqrt(((n - 1)k_1u)/((u + v)v))`.
APPEARS IN
संबंधित प्रश्न
A double convex lens is made of a glass of refractive index 1.55, with both faces of the same radius of curvature. Find the radius of curvature required, if the focal length is 20 cm.
Can mirrors give rise to chromatic aberration?
The image of an extended object, placed perpendicular to the principal axis of a mirror, will be erect if
(a) the object and the image are both real
(b) the object and the image are both virtual
(c) the object is real but the image is virtual
(d) the object is virtual but the image is real.
How can the spherical aberration produced by a lens be minimized?
A thin converging lens of focal length 12 cm is kept in contact with a thin diverging lens of focal length 18 cm. Calculate the effective/equivalent focal length of the combination.
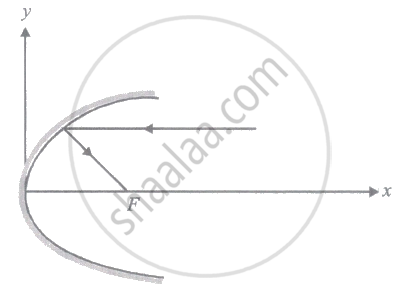
A parallel beam of light ray parallel to the x-axis is incident on a parabolic reflecting surface x = 2by2 as shown in the figure. After reflecting it passes through focal point F. What is the focal length of the reflecting surface?
You are given four sources of light each one providing a light of a single colour – red, blue, green and yellow. Suppose the angle of refraction for a beam of yellow light corresponding to a particular angle of incidence at the interface of two media is 90°. Which of the following statements is correct if the source of yellow light is replaced with that of other lights without changing the angle of incidence?
A short object of length L is placed along the principal axis of a concave mirror away from focus. The object distance is u. If the mirror has a focal length f, what will be the length of the image? You may take L << |v – f|.
An object is 20 cm away from a concave mirror and it is within the focal length of the mirror. If the mirror is changed to a plane mirror, the image moves 15 cm closer to the mirror.
Focal length of the concave mirror is ______.
A concave mirror of focal length 12 cm forms three times the magnified virtual image of an object. Find the distance of the object from the mirror.
