Advertisements
Advertisements
प्रश्न
A double convex lens is made of a glass of refractive index 1.55, with both faces of the same radius of curvature. Find the radius of curvature required, if the focal length is 20 cm.
उत्तर
Refractive index of glass, μ=1.55
Focal length of the double-convex lens, f=20 cm
Radius of curvature of one face of the lens =R1
Radius of curvature of the other face of the lens =R2
Radius of curvature of the double-convex lens = R
∴ R1=R and R2=-R
The value of R can be calculated as:
`1/f=(mu-1)[1/R_1-1/R_2]`
`1/20=(1.55-1)[1/R+1/R]`
`1/20=(0.55)[2/R]`
`therefore R=22 cm`
Hence , the radius of curvature of the double-convex lens is 22 cm
संबंधित प्रश्न
A converging lens of focal length 40 cm is kept in contact with a diverging lens of focal length 30 cm. Find the focal length of the combination .
State how the focal length of a glass lens (Refractive Index 1.5) changes when it is completely immersed in:
(i) Water (Refractive Index 1.33)
(ii) A liquid (Refractive Index 1.65)
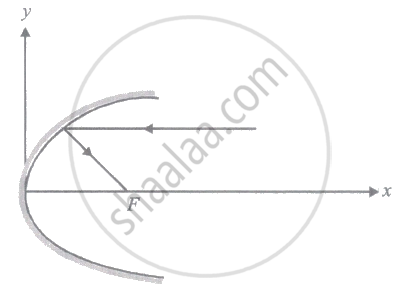
A parallel beam of light ray parallel to the x-axis is incident on a parabolic reflecting surface x = 2by2 as shown in the figure. After reflecting it passes through focal point F. What is the focal length of the reflecting surface?
The radius of curvature of the curved surface of a plano-convex lens is 20 cm. If the refractive index of the material of the lens be 1.5, it will ______.
A car is moving with at a constant speed of 60 km h–1 on a straight road. Looking at the rear view mirror, the driver finds that the car following him is at a distance of 100 m and is approaching with a speed of 5 km h–1. In order to keep track of the car in the rear, the driver begins to glance alternatively at the rear and side mirror of his car after every 2 s till the other car overtakes. If the two cars were maintaining their speeds, which of the following statement (s) is/are correct?
An astronomical refractive telescope has an objective of focal length 20 m and an eyepiece of focal length 2 cm.
- The length of the telescope tube is 20.02 m.
- The magnification is 1000.
- The image formed is inverted.
- An objective of a larger aperture will increase the brightness and reduce chromatic aberration of the image.
A thin convex lens of focal length 25 cm is cut into two pieces 0.5 cm above the principal axis. The top part is placed at (0, 0) and an object placed at (– 50 cm, 0). Find the coordinates of the image.
(i) Consider a thin lens placed between a source (S) and an observer (O) (Figure). Let the thickness of the lens vary as `w(b) = w_0 - b^2/α`, where b is the verticle distance from the pole. `w_0` is a constant. Using Fermat’s principle i.e. the time of transit for a ray between the source and observer is an extremum, find the condition that all paraxial rays starting from the source will converge at a point O on the axis. Find the focal length.
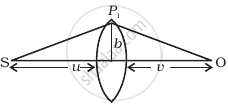
(ii) A gravitational lens may be assumed to have a varying width of the form
`w(b) = k_1ln(k_2/b) b_("min") < b < b_("max")`
= `k_1ln (K_2/b_("min")) b < b_("min")`
Show that an observer will see an image of a point object as a ring about the center of the lens with an angular radius
`β = sqrt((n - 1)k_1 u/v)/(u + v)`
An object is 20 cm away from a concave mirror and it is within the focal length of the mirror. If the mirror is changed to a plane mirror, the image moves 15 cm closer to the mirror.
Focal length of the concave mirror is ______.
A converging lens has a focal length of 10 cm in air. It is made of a material with a refractive index of 1.6. If it is immersed in a liquid of refractive index 1.3, find its new focal length.
