Advertisements
Advertisements
प्रश्न
A small object is embedded in a glass sphere (μ = 1.5) of radius 5.0 cm at a distance 1.5 cm left to the centre. Locate the image of the object as seen by an observer standing (a) to the left of the sphere and (b) to the right of the sphere.
उत्तर
Given,
Radius of the sphere = 5.0 cm
Refractive index of the sphere (μ1) = 1.5
An object is embedded in the glass sphere 1.5 cm left to the centre.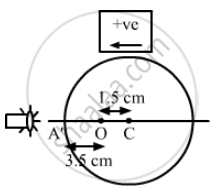
(a)
When the image is seen by observer from left of the sphere,
from surface the object distance (u) = − 3.5 cm
μ1 = 1.5
μ2 = 1
v1 = ?
Using lens equation:
\[\frac{\mu_2}{v_1} - \frac{\mu_1}{u} = \frac{\mu_2 - \mu_1}{R}\]
\[\frac{1}{v_1} - \frac{1 . 5}{- (3 . 5)} = \frac{- 0 . 5}{- 5}\]
\[\frac{1}{v_1} = \frac{1}{10} - \frac{3}{7}\]
\[= \frac{7 - 30}{70}\]
\[= \frac{- 23}{70}\]
\[v_1 = \frac{- 70}{23} \simeq - 3 \text{ cm }\]
So the image will be formed at 2 cm (5 cm - 3cm) left to centre. 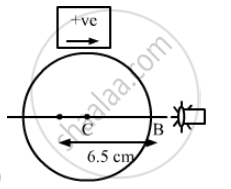
(b) When the image is seen by observer from the right of the sphere,
u = −(5.0 + 1.5) = − 6.5,
R = −5.00 cm
μ1 = 1.5, μ2 = 1, v = ?
Using lens equation:
\[\frac{\mu_2}{v_1} - \frac{\mu_1}{u} = \frac{\mu_2 - \mu_1}{R}\]
\[\frac{1}{v} - \frac{1 . 5}{6 . 3} = \frac{1}{10}\]
\[\frac{1}{v} = \frac{1}{10} - \frac{3}{13}\]
\[= \frac{13 - 30}{130}\]
\[= \frac{- 17}{130}\]
\[v = \frac{- 130}{17} = - 7 . 65 \text{ cm }\]
Therefore, the image will be formed 7.6 − 5 = 2.6 towards left from centre.
APPEARS IN
संबंधित प्रश्न
At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is 1.524.
How does the angle of minimum deviation of a glass prism vary, if the incident violet light is replaced by red light? Give reason.
A ray of light, incident on an equilateral prism `(μ_g = sqrt3)`moves parallel to the base line of the prism inside it. Find the angle of incidence for this ray.
Trace the path of the ray (P) of light passing through the glass prism as shown in the figure. The prism is made of glass with critical angle ic = 41°.
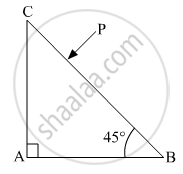
Can you ever have a situation in which a light ray goes undeviated through a prism?
A flint glass prism and a crown glass prism are to be combined in such a way that the deviation of the mean ray is zero. The refractive index of flint and crown glasses for the mean ray are 1.620 and 1.518 respectively. If the refracting angle of the flint prism is 6.0°, what would be the refracting angle of the crown prism?
Find the angle of minimum deviation for an equilateral prism made of a material of refractive index 1.732. What is the angle of incidence for this deviation?
A prism is made of glass of unknown refractive index. A parallel beam of light is incident on the face of the prism. The angle of minimum deviation is measured to be 40°. What is the refractive index of the material of the prism? The refracting angle of the prism is 60°. If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light.
The refractive index of a prism whose angle A = 60° is `sqrt2`. Then the angle of minimum deviation δm will be ______.
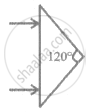
An isosceles prism of angle 120° has a refractive index 1.44. Two parallel monochromatic rays enter the prism parallel to each other in air as shown. The rays emerge from the opposite faces:
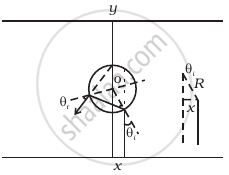
An infinitely long cylinder of radius R is made of an unusual exotic material with refractive index –1 (Figure). The cylinder is placed between two planes whose normals are along the y direction. The center of the cylinder O lies along the y-axis. A narrow laser beam is directed along the y direction from the lower plate. The laser source is at a horizontal distance x from the diameter in the y direction. Find the range of x such that light emitted from the lower plane does not reach the upper plane.
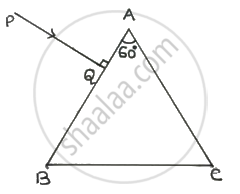
A ray PQ is incident normally on the face AB of a triangular prism of refracting angle 60° as shown in figure. The prism is made of a transparent material of refractive index `2/sqrt(3)`. Trace the path of the ray as it passes through the prism. Calculate the angle of emergence and the angle of deviation.
Two prisms ABC and DBC are arranged as shown in the figure.

The critical angles for the two prisms with respect to air are 41.1° and 45° respectively. Trace the path of the ray through the combination.
The maximum value of the index of refraction of a material of a prism which allows the passage of light through it when the refracting angle of the prism is A is ______.
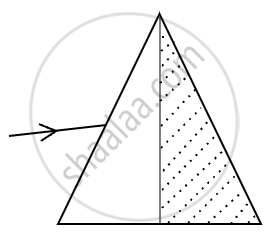
A ray of light when incident upon a thin prism suffers a minimum deviation of 39°. If the shaded half portion of the prism is removed, then the same ray will ______.
A ray of light is refracted by a glass prism. Obtain an expression for the refractive index of the glass in terms of the angle of prism A and the angle of minimum deviation δm.
