Advertisements
Advertisements
प्रश्न
Calculate the maximum kinetic energy of photoelectrons emitted by a metal (work function = 1.5 eV) when it is illuminated with light of wavelength 198 nm.
उत्तर
According to Einstein's photoelectric equation,
`"E"_k = hv - w = (hc)/lambda - w`
Here h = 6.6 × 10-34 Js
c = 3.0 × 108 ms-1
λ = 198 × 10-9 m
w = 1.5 × 1.6 × 10-19 J
`therefore "E"_k = ((6.6 xx 10^-34 xx 3.0 xx 10^8)/(198 xx 10^-9) - 1.5 xx 1.6 xx 10^-19)`J
= (10 × 10-19 - 2.4 × 10-19) J
= 7.6 × 10-19 J
APPEARS IN
संबंधित प्रश्न
When radiations of wavelength λ1 and λ2 are incident on certain photosensitive, such that E1 > E2 . Then Planck's constant 'h' is ......................... .
(C = Velocity of light).
Write Einstein's photoelectric equation and mention which important features in photoelectric effect can be explained with the help of this equation.
The maximum kinetic energy of the photoelectrons gets doubled when the wavelength of light incident on the surface changes from λ1 to λ2. Derive the expressions for the threshold wavelength λ0 and work function for the metal surface.
A proton and a deuteron are accelerated through the same accelerating potential. Which one of the two has less momentum?
Give reasons to justify your answer.
Einstein's photoelectric equation is:
a) `E_"max" = hlambda - varphi_0`
b) `E_"max"= (hc)/lambda varphi_0`
c) `E_"max" = hv + varphi_0`
d) `E_"max" = (hv)/lambda + varphi_0`
Write Einstein’s photoelectric equation.
Which of the following graphs correctly represents the variation of maximum kinetic energy (Ek) of photoelectrons with the frequency (𝜈) of the incident radiation?
A police van moving on a highway with a speed of 30 km/h fires a bullet at a thief's car speeding away in the same direction with a speed of 192 km/h. If the muzzle speed of the bullet is 150 m is, with what speed does the bullet hit the thief's car?
Radiations of two photon's energy, twice and ten times the work function of metal are incident on the metal surface successively. The ratio of maximum velocities of photoelectrons emitted in two cases is:
A 200 W sodium street lamp emits yellow light of wavelength 0.6 µm. Assuming it to be 25% efficient in converting electrical energy to light, the number of photons of yellow light it emits per second is:
The graphs below show the variation of the stopping potential VS with the frequency (ν) of the incident radiations for two different photosensitive materials M1 and M2.
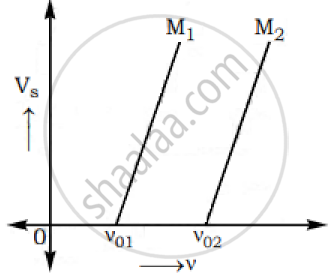
Express work function for M1 and M2 in terms of Planck’s constant(h) and Threshold frequency and charge of the electron (e).
If the values of stopping potential for M1 and M2 are V1 and V2 respectively then show that the slope of the lines equals to `(V_1-V_2)/(V_(01)-V_(02))` for a frequency,
ν > ν02 and also ν > ν01
