Advertisements
Advertisements
प्रश्न
Calculate the work involved in the expansion and compression process.
उत्तर
Work involved in expansion and compression processes:
In most thermodynamic calculations we are dealing with the evaluation of work involved in the expansion or compression of gases. The essential condition for expansion or compression of a system; is that there should be a difference between external pressure (Pext) and internal pressure (Pint).
For understanding pressure-volume work, let us consider a cylinder that contains V moles of an ideal gas fitted with a frictionless piston of cross-sectional area A. The total volume of the gas inside is V and the pressure of the gas inside is Pint. If the external pressure Pext is greater than Pint, the piston moves inward till the pressure inside becomes equal to Pext. Let this change be achieved in a single step
and the final volume be Vf. In this case, the work is done on the system (+w). It can be calculated as follows
w = − F.∆x ……….(1)
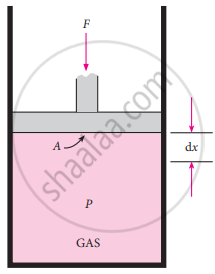
showing work involved in compression processes
F = PextA ……….(2)
Substituting (2) in (1)
w = – Pext. A. ∆x
A .∆x = change in volume = Vf – Vi
w = − Pext.(Vf – Vi) ……….(3)
w = − Pext. (− ∆V) …………(4)
= Pext.∆V
Since work is done on the system, it is a positive quantity.
If the pressure is not constant, but changes during the process such that it is always infinitesimally greater than the pressure of the gas, then, at each stage of compression, the volume decreases by an infinitesimal amount, dV. In such a case we can calculate the work done on the gas by the relation
Wrev = – `∫_("V"_"i")^("V"_"f")` pext dV
In a compression process, Pext the external pressure is always greater than the pressure of the system.
i.e., Pext = (Pint + dP)
In an expansion process, the external pressure is always less than the pressure of the system
i.e., Pext = (Pint – dP)
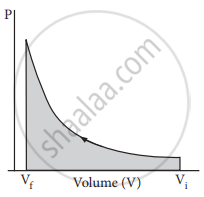
When pressure is not constant and changes in infinitesimally small steps (reversible conditions) during compression from Vi to Vf. the P-V plot looks like in the figure. Work done on the gas is represented by the shaded area.
In the general case, we can write,
Pext = (Pint ± dP). Such processes are called reversible processes. For a compression process work can be related to internal pressure of the system under reversible conditions by writing equation
Wrev = – `∫_("V"_"i")^("V"_"f")` Pint dV
For a given system with an ideal gas
Pint V = nRT
pint = `"nRT"/"V"`
Wrev = – `∫_("V"_"i")^("V"_"f") "nRT"/"V"` dV
Wrev = – nRT `∫_("V"_"i")^("V"_"f") ("dV"/"V")`
Wrev= – nRT ln `("V"_"f"/"V"_"i")`
Wrev= – 2.303 nRT log `("V"_"f"/"V"_"i")` ........(5)
If Vf > Vi (expansion), the sign of work done by the process is negative.
If Vf < Vi (compression) the sign of work done on the process is positive.
APPEARS IN
संबंधित प्रश्न
In an adiabatic process, which of the following is true?
In a reversible process, the change in entropy of the universe is
In an adiabatic expansion of an ideal gas
The intensive property among the quantities below is
Change in internal energy, when 4 kJ of work is done on the system and 1 kJ of heat is given out by the system is
In an isothermal reversible compression of an ideal gas the sign of q, ∆S and w are respectively
Explain intensive properties with two examples.
Define the following term:
Isothermal process
Define the following term:
Adiabatic process
Define the following term:
Isochoric process
