Advertisements
Advertisements
प्रश्न
Choose the correct answer of the following question:
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
विकल्प
1 : 2
1 : 4
1 : 6
1 : 8
उत्तर
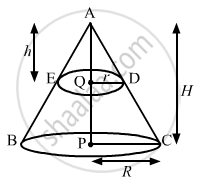
Let the radii of the smaller and given cones be r and R, respectively; and their heights b and H respectively
We have,
H = 2h .........(i)
In ΔAQD and ΔAPC,
∠QAD = ∠PAC (common angle)
∠AQD = ∠APC = 90°
So, by AA citeria
Δ AQD ˜ Δ APC
`=> "AQ"/"AP" = "QD"/"PC"`
`=> "h"/"H" = "r"/"R"`
`=> "h"/"2h" = "r"/"R"`
`=>1/2 = "r"/"R"`
⇒ R = 2r ........(ii)
Now,
The ratio of the smaller cone to the whole cone`="Volume of the smaller cone"/"Volume of the whole cone"`
`= ((1/3pi"r"^2"h"))/((1/3pi"R"^2H))`
`=("r"/"R")^2 xx ("h"/"H")`
`=("r"/"2r")^2xx("h"/"2h")` [Using (i) and (ii)]
`=(1/2)^2 xx (1/2)`
`=1/8`
= 1 : 8
Hence, the correct answer is option (d).
APPEARS IN
संबंधित प्रश्न
A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel of base radius 10 cm. Find the height to which the water will rise in the cylindrical vessel. (use `pi=22/7`)
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3.
The `3/4` th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel.
A cylindrical tank full of water is emptied by a pipe at the rate of 225 litres per minute. How much time will it take to empty half the tank, if the diameter of its base is 3 m and its height is 3.5 m? [Use \[\pi = \frac{22}{7}\]]
A pen stand made of wood is in the shape of a cuboid with four conical depression and a cubical depression to hold the pens and pins , respectively . The dimension of the cuboid are \[10 cm \times 5 cm \times 4 cm\].
The radius of each of the conical depression is 0.5 cm and the depth is 2.1 cm . The edge of the cubical depression is 3 cm . Find the volume of the wood in the entire stand.
In the middle of a rectangular field measuring 30 m × 20 m, a well of 7 m diameter and 10 m depth is dug. The earth so removed is evenly spread over the remaining part of the field. Find the height through which the level of the field is raised.
An iron pillar consists of a cylindrical portion 2.8 m high and 20 cm in diameter and a cone 42 cm high is surmounting it. Find the weight of the pillar, given that 1 cubic cm of iron weighs 7.5 gm.
Three cubes of iron whose edges are 6 cm, 8 cm and 10 cm, respectively are melted and formed into a single cube. Find the edge of the new cube formed.
The length, breadth and height of a cuboidal reservoir is 7 m, 6 m and 15 m respectively. 8400 L of water is pumped out from the reservoir. Find the fall in the water level in the reservoir.
The internal and external radii of a spherical shell are 3cm and 5cm respectively. It is melted and recast into a solid cylinder of diameter 14 cm, find the height of the cylinder. Also find the total surface area of the cylinder. (Take `pi = 22/7`)
