Advertisements
Advertisements
प्रश्न
| Column A | Column B |
| (a) If E1 and E2 are the two mutually exclusive events | (i) E1 ∩ E2 = E1 |
| (b) If E1 and E2 are the mutually exclusive and exhaustive events | (ii) (E1 – E2) ∪ (E1 ∩ E2) = E1 |
| (c) If E1 and E2 have common outcomes, then | (iii) E1 ∩ E2 = Φ, E1 ∪ E2 = S |
| (d) If E1 and E2 are two events such that E1 ⊂ E2 | (iv) E1 ∩ E2 = Φ |
उत्तर
| Column A | Column B |
| (a) If E1 and E2 are the two mutually exclusive events | (iv) E1 ∩ E2 = Φ |
| (b) If E1 and E2 are the mutually exclusive and exhaustive events | (iii) E1 ∩ E2 = Φ, E1 ∪ E2 = S |
| (c) If E1 and E2 have common outcomes, then | (ii) (E1 – E2) ∪ (E1 ∩ E2) = E1 |
| (d) If E1 and E2 are two events such that E1 ⊂ E2 | (i) E1 ∩ E2 = E1 |
Explanation:
(a) If E1 and E2 are mutually exclusive events, then E1 ∩ E2 = Φ.
(b) If E1 and E2 are mutually exclusive and exhaustive events then E1 ∩ E2 = Φ and E1 ∪ E2 = S.
(c) If E1 and E2 have common outcomes, then (E1 – E2) ∪ (E1 ∩ E2) = E1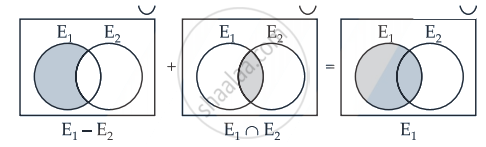
(d) If E1 and E2 are two events such that
E1 ⊂ E2 ⇒ E1 ∩ E2 = E1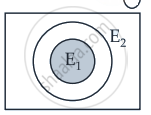
APPEARS IN
संबंधित प्रश्न
Two dice are thrown. The events A, B and C are as follows:
A: getting an even number on the first die.
B: getting an odd number on the first die.
C: getting the sum of the numbers on the dice ≤ 5
State true or false: (give reason for your answer).
A = B'
Two dice are thrown. The events A, B and C are as follows:
A: getting an even number on the first die.
B: getting an odd number on the first die.
C: getting the sum of the numbers on the dice ≤ 5
State true or false: (give reason for your answer)
A and C are mutually exclusive
Two dice are thrown. The events A, B and C are as follows:
A: getting an even number on the first die.
B: getting an odd number on the first die.
C: getting the sum of the numbers on the dice ≤ 5
State true or false: (give reason for your answer)
A and B' are mutually exclusive
Given P(A) = `3/5` and P(B) = `1/5`. Find P(A or B), if A and B are mutually exclusive events.
Three coins are tossed. Describe. three events A, B and C which are mutually exclusive and exhaustive.
Three coins are tossed. Describe.
(iv) two events A and B which are mutually exclusive but not exhaustive.
A die is thrown twice. Each time the number appearing on it is recorded. Describe the following events:
A = Both numbers are odd.
B = Both numbers are even.
C = sum of the numbers is less than 6
Also, find A ∪ B, A ∩ B, A ∪ C, A ∩ C
Which pairs of events are mutually exclusive?
Two dice are thrown. The events A, B, C, D, E and F are described as :
A = Getting an even number on the first die.
B = Getting an odd number on the first die.
C = Getting at most 5 as sum of the numbers on the two dice.
D = Getting the sum of the numbers on the dice greater than 5 but less than 10.
E = Getting at least 10 as the sum of the numbers on the dice.
F = Getting an odd number on one of the dice.
Describe the event:
A and B, B or C, B and C, A and E, A or F, A and F
Two dice are thrown. The events A, B, C, D, E and F are described as:
A = Getting an even number on the first die.
B = Getting an odd number on the first die.
C = Getting at most 5 as sum of the numbers on the two dice.
D = Getting the sum of the numbers on the dice greater than 5 but less than 10.
E = Getting at least 10 as the sum of the numbers on the dice.
F = Getting an odd number on one of the dice.
State true or false:
- A and B are mutually exclusive.
- A and B are mutually exclusive and exhaustive events.
- A and C are mutually exclusive events.
- C and D are mutually exclusive and exhaustive events.
- C, D and E are mutually exclusive and exhaustive events.
- A' and B' are mutually exclusive events.
- A, B, F are mutually exclusive and exhaustive events.
If A and B be mutually exclusive events associated with a random experiment such that P(A) = 0.4 and P(B) = 0.5, then find
P (A ∪ B)
If A and B be mutually exclusive events associated with a random experiment such that P(A) = 0.4 and P(B) = 0.5, then find
\[P (\bar{ A } \cap \bar{ B} )\]
If A and B be mutually exclusive events associated with a random experiment such that P(A) = 0.4 and P(B) = 0.5, then find
P (A ∩\[\bar{ B } \] ).
From a well shuffled deck of 52 cards, 4 cards are drawn at random. What is the probability that all the drawn cards are of the same colour.
A box contains 10 white, 6 red and 10 black balls. A ball is drawn at random from the box. What is the probability that the ball drawn is either white or red?
The probability that a person will travel by plane is 3/5 and that he will travel by trains is 1/4. What is the probability that he (she) will travel by plane or train?
A box contains 30 bolts and 40 nuts. Half of the bolts and half of the nuts are rusted. If two items are drawn at random, what is the probability that either both are rusted or both are bolts?
If A and B are mutually exclusive events such that P(A) = 0.35 and P(B) = 0.45, find P(A ∩ \[\bar{ B } \] )
If A and B are mutually exclusive events such that P(A) = 0.35 and P(B) = 0.45, find P(\[\bar{ A } \] ∩ \[\bar{B} \] )
If \[\frac{(1 - 3p)}{2}, \frac{(1 + 4p)}{3}, \frac{(1 + p)}{6}\] are the probabilities of three mutually exclusive and exhaustive events, then the set of all values of p is
If S is the sample space and P(A) = \[\frac{1}{3}\] P(B) and S = A ∪ B, where A and B are two mutually exclusive events, then P (A) =
If A and B are mutually exclusive events then
An experiment has four possible outcomes A, B, C and D, that are mutually exclusive. Explain why the following assignments of probabilities are not permissible:
P(A) = 0.12, P(B) = 0.63, P(C) = 0.45, P(D) = – 0.20
An experiment has four possible outcomes A, B, C and D, that are mutually exclusive. Explain why the following assignments of probabilities are not permissible:
P(A) = `9/120`, P(B) = `45/120`, P(C) = `27/120`, P(D) = `46/120`
A die is loaded in such a way that each odd number is twice as likely to occur as each even number. Find P(G), where G is the event that a number greater than 3 occurs on a single roll of the die.
If A and B are mutually exclusive events, P(A) = 0.35 and P(B) = 0.45, find P(B′)
If A and B are mutually exclusive events, P(A) = 0.35 and P(B) = 0.45, find P(A ∩ B)
The probability of happening of an event A is 0.5 and that of B is 0.3. If A and B are mutually exclusive events, then the probability of neither A nor B is ______.
If the events A and B are mutually exclusive events such that P(A) = `(3x + 1)/3` and P(B) = `(1 - x)/4`, then the set of possible values of x lies in the interval ______.
