Advertisements
Advertisements
प्रश्न
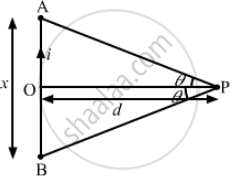
Consider a straight piece of length x of a wire carrying a current i. Let P be a point on the perpendicular bisector of the piece, situated at a distance d from its middle point. Show that for d >> x, the magnetic field at P varies as 1/d2 whereas for d << x, it varies as 1/d.
उत्तर
Let AB be the wire of length x with midpoint O.
Given:
Magnitude of current = i
Separation of the point from the wire = d
Now,
The magnetic field on a perpendicular bisector is given by
\[ \Rightarrow B \propto \frac{1}{d^2}\]
\[ \Rightarrow B \propto \frac{1}{d}\]
APPEARS IN
संबंधित प्रश्न
A short bar magnet of magnetic moment 0.9 J/T is placed with its axis at 30° to a uniform magnetic field. It experiences a torque of 0.063 J.
(i) Calculate the magnitude of the magnetic field.
(ii) In which orientation will the bar magnet be in stable equilibrium in the magnetic field?
A particle moves in a region with a uniform magnetic field and a parallel, uniform electric field. At some instant, the velocity of the particle is perpendicular to the field direction. The path of the particle will be
You are facing a circular wire carrying an electric current. The current is clockwise as seen by you. Is the field at the centre coming towards you or going away from you?
Two parallel wires carry currents of 20 A and 40 A in opposite directions. Another wire carying a current anti parallel to 20 A is placed midway between the two wires. T he magnetic force on it will be
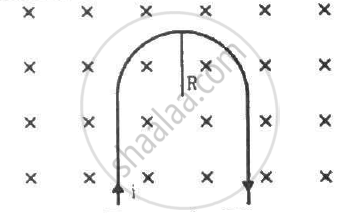
A rigid wire consists of a semi-circular portion of radius R and two straight sections (figure). The wire is partially immersed in a perpendicular magnetic field B, as shown in the figure. Find the magnetic force on the wire if it carries a current i.
Consider a non-conducting plate of radius r and mass m that has a charge q distributed uniformly over it. The plate is rotated about its axis with an angular speed ω. Show that the magnetic moment µ and the angular momentum l of the plate are related as `mu = q/(2 m)l`
Consider a solid sphere of radius r and mass m that has a charge q distributed uniformly over its volume. The sphere is rotated about its diameter with an angular speed ω. Show that the magnetic moment µ and the angular momentum l of the sphere are related as `mu = q/(2m) l`
A long wire carrying a current i is bent to form a place along α . Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex.
A long, straight wire is fixed horizontally and carries a current of 50.0 A. A second wire having linear mass density 1.0 × 10−4 kg m−1 is placed parallel to and directly above this wire at a separation of 5.0 mm. What current should this second wire carry such that the magnetic repulsion can balance its weight?
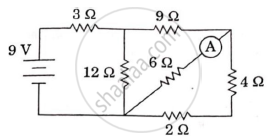
In the circuit shown in the figure, find the value of the current shown in the ammeter A.
An electron is projected with uniform velocity along the axis of a current carrying long solenoid. Which of the following is true?
When a magnetic compass needle is carried nearby to a straight wire carrying current, then
- the straight wire cause a noticeable deflection in the compass needle.
- the alignment of the needle is tangential to an imaginary circle with straight wire as its centre and has a plane perpendicular to the wire.
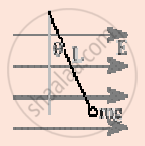
A small object with charge q and weight mg is attached to one end of a string of length ‘L’ attached to a stationary support. The system is placed in a uniform horizontal electric field ‘E’, as shown in the accompanying figure. In the presence of the field, the string makes a constant angle θ with the vertical. The sign and magnitude of q ______.
A conducting ring of radius 1m kept in a uniform magnetic field B of 0.01 T, rotates uniformly with an angular velocity 100 rad s−1 with its axis of rotation perpendicular to B. The maximum induced emf in it is:
A conducting loop of resistance R and radius r has its centre at the origin of the coordinate system in a magnetic field of induction B. When it is rotated about y-axis through 90°, the net charge flown in the loop is directly proportional to: