Advertisements
Advertisements
प्रश्न
Derive an expression for variation in gravitational acceleration of the Earth at with latitude.
उत्तर
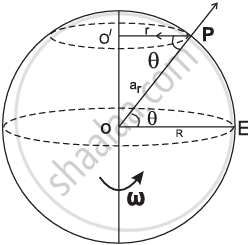 |
| Variation of g with latitude |
- Latitude is an angle made by the radius vector of any point from the center of the Earth with the equatorial plane.
- The Earth rotates about its polar axis from west to east with uniform angular velocity ω as shown in the figure.
Hence, every point on the surface of the Earth (except the poles) moves in a circle parallel to the equator. - The motion of a mass m at point P on the Earth is shown by the dotted circle with the center at O′.
- Let the latitude of P be θ and the radius of the circle be r.
∴ PO' = r
∠EOP = θ, E being a point on the equator
∴ ∠OPO' = θ
In Δ OPO', cos θ = `"PO'"/"PO" = "r"/"R"`
∴ r = R cos θ - The centripetal acceleration for the mass m, directed along PO' is,
a = rω2
∴ a = rω2 cos θ
The component of this centripetal acceleration along PO, i.e., towards the centre of the Earth is,
`"a"_"r" = "a" cos theta`
∴ `"a"_"r" = "R"omega^2 cos theta xx cos theta`
`"a"_"r" = "R"omega^2cos^2theta` - Part of the gravitational force of attraction on P acting towards PO is utilized in providing this component of centripetal acceleration. Thus, the effective force of gravitational attraction on m at P can be written as,
mg' = mg - mRω2cos2θ
Thus, the effective acceleration due to gravity at P is given as,
g' = g - Rω2cos2θ
APPEARS IN
संबंधित प्रश्न
Answer the following question.
What is the variation in acceleration due to gravity with altitude?
Answer the following question in detail.
Show that acceleration due to gravity at height h above the Earth’s surface is `"g"_"h" = "g"("R"/"R + h")^2`
Answer the following question in detail.
Draw a graph showing the variation of gravitational acceleration due to the depth and altitude from the Earth’s surface.
Answer the following question in detail.
At which place on the Earth’s surface is the gravitational acceleration minimum? Why?
Answer the following question in detail.
Obtain the formula for the acceleration due to gravity at the depth ‘d’ below the Earth’s surface.
Answer the following question in detail.
State the formula for the acceleration due to gravity at depth ‘d’ and altitude ‘h’. Hence show that their ratio is equal to `(("R - d")/("R - 2h"))` by assuming that the altitude is very small as compared to the radius of the Earth.
At what distance below the surface of the Earth, the acceleration due to gravity decreases by 10% of its value at the surface, given the radius of Earth is 6400 km.
At what height h above earth, the value of g becomes `g/2` (where R = radius of earth)?
Calculate angular velocity of earth so that acceleration due to gravity at 60° latitude becomes zero. (Radius of earth = 6400 km, gravitational acceleration at poles = 10 m/s2, cos 60° = 0.5)
A clock 'S' is working on oscillations of a spring and a clock 'P' is working on pendulum motion. Both clocks are running at the same rate on earth. What will happen to their functioning on a planet which has the same density as that of earth, but the radius is twice that of earth?
Three-point masses, each of mass 'm' are kept at the comers of an equilateral triangle of side 'L'. The system rotates about the centre of the triangle without any change in the eparation of masses during rotation. The period of rotation is directly proportional to ______.
`(cos30^circ=sin60^circ=sqrt3/2, cos60^circ=sin30^circ=1/2)`
A mass 'm' suspended from a spring stretches it by 5cm when on the surface of the earth. The mass is then taken on to a height of 1600 km above earth's surface and again suspended from the same spring. At this altitude the extension of the spring is ______.
(Radius of earth = 6400 km)
The speed with which the earth would have to rotate about its axis so that a person on the equator would weight `3/5`th as much at present is ______.
(g = gravitational acceleration, R = equatorial radius of the earth)
