Advertisements
Advertisements
प्रश्न
(a) Derive an expression for the electric field E due to a dipole of length '2a' at a point distant r from the centre of the dipole on the axial line.
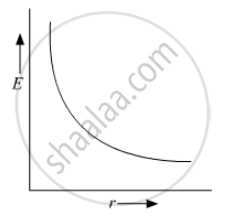
(b) Draw a graph of E versus r for r >> a.
(c) If this dipole were kept in a uniform external electric field E0, diagrammatically represent the position of the dipole in stable and unstable equilibrium and write the expressions for the torque acting on the dipole in both the cases.
उत्तर
(a) Electric Field on Axial Line of an Electric Dipole:
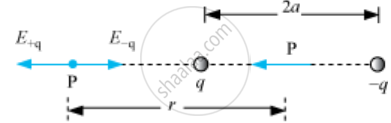
Let P be at distance r from the centre of the dipole on the side of charge q. Then,
`E_(-q)=q/(4piepsilon_0(r+a)^2)hatp`
Where, `hatp` is the unit vector along the dipole axis (from − q to q). Also,
`E_(+q)=q/(4piepsilon_0(r-a)^2)hatp`
The total field at P is
`E=E_(+q)+E_(-q)=q/(4piepsilon_0)[1/(r-a)^2-1/(r+a)^2]hatp`
`E=q/(4piepsilon_0)(4ar)/(r^2-a^2)^2hatp`
for r >> a
`E=(4qa)/(4piepsilon_0r^3)hatp` (r >> a)
`E=(2p)/(4piepsilon_0r^3)` `[because vecp=qxxvec(2a)hatp]`
(b) For r >> a, `E prop 1/r^3`
(c) Position of dipole in stable equilibrium: In stable equilibrium, dipole aligns itself in the direction of external electric field.
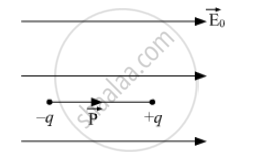
Therefore, angle (θ) between `vecP` and `vecE_0` is 0 and we know torque acting on the dipole in an external field is given by the expression
τ = PEsinθ
As, θ is 0° for stable equilibrium
Therefore, τ = PEsinθ
τ= PEsin0°
τ = 0
Position of dipole in unstable equilibrium: In unstable equilibrium, dipole aligns itself in the direction opposite to the direction of external electric field.
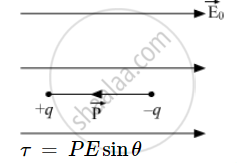
τ = PEsinθ
As, θ is 180° for unstable equilibrium
Therefore, τ = PEsinθ
τ= PEsin180°
τ = 0
संबंधित प्रश्न
Why do the electrostatic field lines not form closed loops?
- An electrostatic field line is a continuous curve. That is, a field line cannot have sudden breaks. Why not?
- Explain why two field lines never cross each other at any point?
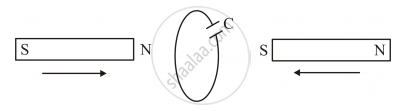
Two bar magnets are quickly moved towards a metallic loop connected across a capacitor ‘C’ as shown in the figure. Predict the polarity of the capacitor.
A thin, metallic spherical shell contains a charge Q on it. A point charge q is placed at the centre of the shell and another charge q1 is placed outside it as shown in the following figure. All the three charges are positive. The force on the central charge due to the shell is ______.
Answer the following question.
Draw the pattern of electric field lines when a point charge +q is kept near an uncharged conducting plate.
Answer the following question.
Derive an expression for the electric field due to a dipole of dipole moment `vec"p"` at a point on its perpendicular bisector.
Explain why two field lines never cross each other at any point?
If Ea be the electric field strength of a short dipole at a point on its axial line and Ee that on the equatorial line at the same distance, then:
Figure shows the electric field lines around three point charges A, B and C.

- Which charges are positive?
- Which charge has the largest magnitude? Why?
- In which region or regions of the picture could the electric field be zero? Justify your answer.
(i) near A, (ii) near B, (iii) near C, (iv) nowhere.
The magnitude of the electric field due to a point charge object at a distance of 4.0 m is 9 N/C. From the same charged object the electric field of magnitude, 16 N/C will be at a distance of ______.
