Advertisements
Advertisements
Question
(a) Derive an expression for the electric field E due to a dipole of length '2a' at a point distant r from the centre of the dipole on the axial line.
(b) Draw a graph of E versus r for r >> a.
(c) If this dipole were kept in a uniform external electric field E0, diagrammatically represent the position of the dipole in stable and unstable equilibrium and write the expressions for the torque acting on the dipole in both the cases.
Advertisements
Solution
(a) Electric Field on Axial Line of an Electric Dipole:
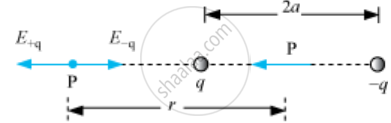
Let P be at distance r from the centre of the dipole on the side of charge q. Then,
`E_(-q)=q/(4piepsilon_0(r+a)^2)hatp`
Where, `hatp` is the unit vector along the dipole axis (from − q to q). Also,
`E_(+q)=q/(4piepsilon_0(r-a)^2)hatp`
The total field at P is
`E=E_(+q)+E_(-q)=q/(4piepsilon_0)[1/(r-a)^2-1/(r+a)^2]hatp`
`E=q/(4piepsilon_0)(4ar)/(r^2-a^2)^2hatp`
for r >> a
`E=(4qa)/(4piepsilon_0r^3)hatp` (r >> a)
`E=(2p)/(4piepsilon_0r^3)` `[because vecp=qxxvec(2a)hatp]`
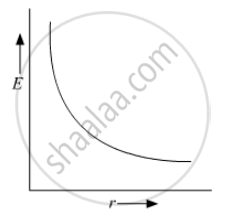
(b) For r >> a, `E prop 1/r^3`
(c) Position of dipole in stable equilibrium: In stable equilibrium, dipole aligns itself in the direction of external electric field.
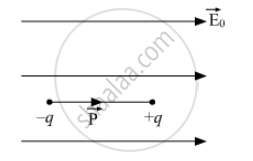
Therefore, angle (θ) between `vecP` and `vecE_0` is 0 and we know torque acting on the dipole in an external field is given by the expression
τ = PEsinθ
As, θ is 0° for stable equilibrium
Therefore, τ = PEsinθ
τ= PEsin0°
τ = 0
Position of dipole in unstable equilibrium: In unstable equilibrium, dipole aligns itself in the direction opposite to the direction of external electric field.
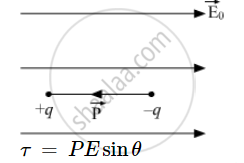
τ = PEsinθ
As, θ is 180° for unstable equilibrium
Therefore, τ = PEsinθ
τ= PEsin180°
τ = 0
RELATED QUESTIONS
Which among the curves shown in the fig. cannot possibly represent electrostatic field lines?
(a)
(b)
(c)
(d)
(e)
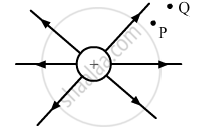
The figure shows the field lines on a positive charge. Is the work done by the field in moving a small positive charge from Q to P positive or negative? Give reason.
Two bar magnets are quickly moved towards a metallic loop connected across a capacitor ‘C’ as shown in the figure. Predict the polarity of the capacitor.
A thin, metallic spherical shell contains a charge Q on it. A point charge q is placed at the centre of the shell and another charge q1 is placed outside it as shown in the following figure. All the three charges are positive. The force on the central charge due to the shell is ______.
The intensity of the electric field at a perpendicular distance of 0·5 m from an infinitely long line charge having linear charge density (λ) is 3-6 × 103 Vm-1. Find the value of λ.
Answer the following question.
Derive an expression for the electric field due to a dipole of dipole moment `vec"p"` at a point on its perpendicular bisector.
Figure shows electric field lines in which an electric dipole P is placed as shown. Which of the following statements is correct?
An electron enters an electric field with its velocity in the direction of the electric lines of force. Then ______
In figure, two positive charges q2 and q3 fixed along the y axis, exert a net electric force in the + x direction on a charge q1 fixed along the x-axis. If a positive charge Q is added at (x, 0), the force on q1
 (a) |
 (b) |
