Advertisements
Advertisements
प्रश्न
Derive the conditions for bright and dark fringes produced due to diffraction by a single slit.
उत्तर
When a single slit of finite width is illuminated by a parallel beam of monochromatic light of wavelength λ, we see a broad pattern of alternate dark and bright fringes on a screen some distance from the slit. The pattern is made up of a central bright fringe, followed by dark and bright fringes of diminishing intensity on both sides. This is called the diffraction pattern of a single slit. Consider a single slit that is illuminated by a monochromatic light beam that is parallel to the slit's plane. The diffraction pattern is obtained on a screen at a distance D ( » a) from the slit and at the focal plane of the convex lens,
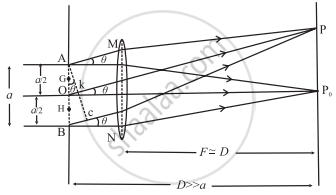
Fraunhofer diffraction due to a single slit
We can imagine the single slit as being made up of a large number of Huygens' sources that are evenly distributed across its width. Then the maxima and minima of the pattern arise from the interference of the various Huygens' wavelets. Consider the single slit as being made up of two adjacent slits, each with a/2 width. All Huygens sources at the slit will be in phase because the incident plane wavefronts are parallel to the slit plane.
They will therefore also in phase at the point P0 on the screen, where P0 is equidistant from all the Huygens sources. At P0 then, we get the central maximum.
For the first minimum of intensity on the screen, the path difference between the waves from the Huygens sources A and O (or 0 and B) is λ/2, which is the condition for destructive interference. Suppose, the nodal line OP for the first minimum subtends an angle θ at the slit; θ is very small. With P as the centre and PA as radius, strike an arc intersecting PB at C. Since, D » a, the arc AC can be considered a straight line at right angles to PB.
Then, Δ ABC is a right-angled triangle similar to Δ OP0P.
This means that, ∠ BAC = θ
∴ BC = a sin θ
∴ Difference in path length,
BC = PB - PA = (PB - PO) + (PO - PA)
=`lambda/2 + lambda/2 = lambda`
∴ a sin θ = λ
∴ sin θ ≅ θ = `lambda/"a"` .....(1)
(∵ θ is very small and in radian)
The other nodal lines of intensity minima can be understood in a similar way. In general, then, for the mth minimum (m = ± 1, ± 2, ± 3,....)
`theta_"m" = ("m"lambda)/"a"` (mth minimum) ...(2)
as θm is very small and in radian.
Between the successive minima, the intensity rises to secondary maxima when the path difference is an odd-integral multiple of `lambda/2`:
a sin θm = (2m + 1)`lambda/2 = ("m" + 1/2) lamda`
i.e., at angles given by,
θm ≅ sin θm = `("m" + 1/2)lambda/"a"`
(mth secondary maximum) ......(3)
APPEARS IN
संबंधित प्रश्न
In a biprism experiment, the fringes are observed in the focal plane of the eyepiece at a distance of 1.2 m from the slits. The distance between the central bright and the 20th bright band is 0.4 cm. When a convex lens is placed between the biprism and the eyepiece, 90 cm from the eyepiece, the distance between the two virtual magnified images is found to be 0.9 cm. Determine the wavelength of light used.
What must be the ratio of the slit width to the wavelength of light for a single slit to have the first diffraction minimum at 45.0°?
A star is emitting light at the wavelength of 5000 Å. Determine the limit of resolution of a telescope having an objective of a diameter of 200 inch.
What should be the slit width to obtain pronounced diffraction with a single slit illuminated by the light of wavelength λ?
What is the difference between Fresnel and Fraunhofer diffraction?
Explain experimental setup for Fraunhofer diffraction with neat diagram.
Explain Fraunhofer diffraction at a single slit with a neat ray diagram. Obtain an expression for the width of the central bright fringe.
Light of wavelength 'λ' is incident on a single slit of width 'a' and the distance between slit and screen is 'D'. In diffraction pattern, if slit width is equal to the width of the central maximum then 'D' is equal to ______.
The luminous border that surrounds the profile of a mountain just before sun rises behind it, is an example of ______.
In Fraunhofer diffraction pattern, slit width is 0.2 mm and screen is at 4 m away from the lens. If wavelength of light used is 5500 Å, then the distance between the first minimum on either side of the central maximum is (`theta` is small and measured in radian) ____________.
In a single slit diffraction pattern, which of the following is incorrect for fringe pattern?
Select the CORRECT statement from the following.
In Fresnel's biprism experiment, when the distance between the slit aperture and eye is increased, then distance between the fringes ____________.
The first minimum of a single slit diffraction pattern is observed at angle 2° with a light of wavelength 510 nm. The width of this slit is ____________.
A parallel beam of monochromatic light falls normally on a single narrow slit. The angular width of the central maximum in the resulting diffraction pattern ______
When two coherent sources in Young's experiment are far apart, then interference pattern ______
A parallel beam of monochromatic light of wavelength 5 × 10-7 m is incident normally on a single narrow slit of width 10-3 mm. At what angle of diffraction, the first minima are observed?
In Young's double slit experiment, the fringe width is 12 mm. If the entire arrangement is placed in water of refractive index `4/3`, then the fringe width becomes (in mm) ______.
In Young's double silt experiment, two slits are d distance apart. The interference pattern is observed on a screen at a distance D from the slits. The first dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light is ______.
A mixture of light, consisting of wavelength 590 nm and an unknown wavelength, illuminates Young's double slit and gives rise to two overlapping intererence patterns on the screen. The central maximum of both lights coincides.
Further, it is observed that the third bright fringe of known light coincides with the 4th bright fringe of the unknown light. From this data the wavelength of the unknown light is ______.
In a Young’s experiment, two coherent sources are placed 0.90 mm apart and the fringes are observed one metre away. If it produces the second dark fringe at a distance of 1mm from the central fringe, then the wavelength of monochromatic light used will be ______.
In Young's double slit experiment, the 8th maximum with wavelength λ1 is at a distance d1 from the central maximum and the 6th maximum with a wavelength λ2 is at a distance d2. Then d1/d2 is equal to ______.
In a Young's double slit experiment carried out with light of wavelength λ = 5000 Å, the distance between the slits is 0.2 mm and the screen is at 200 cm from the slits. The central maximum is at x = 0. The third maximum (taking the central maximum as zeroth maximum) will be at x equal to ______.
The angular width of the central maximum of the diffraction pattern in a single slit (of width a) experiment, with λ as the wavelength of light, is ______.
In a biprism experiment, the slit is illuminated by red light of wavelength 6400 A and the crosswire of eyepiece is adjusted to the centre of 3rd bright band. By using blue light it is found that 4th bright band is at the centre of the cross wire. Calculate the wavelength of blue light.
State the characteristics of a single slit diffraction pattern.
