Advertisements
Advertisements
प्रश्न
Determine whether the following function is differentiable at the indicated values.
f(x) = x |x| at x = 0
उत्तर
`f(x) = {{:(x(- x), "if" x < 0),(x(x), "if" x > 0):}`
`f(x) = {{:(- x^2, "if" x < 0),(x^2, "if" x > 0):}`
To find the left limit of `f(x)` at x = 0
When x → 0
`f(x) = - x^2`
`f"'"(0^-) = lim_(x -> 0^-) (f(x) - f(0))/(x - 0)`
= `lim_(x -> 0^-) (-x^2 - 0^2)/(x - 0)`
= `lim_(x -> 0^-) (-x^2)/x`
= `lim_(x -> 0^-) (- x)` = 0 .........(1)
To find the right limit of `f(x)` at x = 0
When x → 0+
`f(x) = x^2`
`f"'"(0^+) = lim_(x -> 0^+) (f(x) - f(0))/(x - 0)`
= `lim_(x -> 0^+) (x^2 - 0^2)/x`
= `lim_(x -> 0^+) (x^2)/x`
= `lim_(x -> 0^+) x` = 0 .........(2)
From eqation (1) and (2) we get
`f"'"(0-) = f"'"(0^+)`
∴ f(x) is differentiable at x = 0.
APPEARS IN
संबंधित प्रश्न
Find the derivatives of the following functions using first principle.
f(x) = – x2 + 2
Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?
`f(x) = sqrt(1 - x^2)`
Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?
`f(x) = {{:(x",", x ≤ 1),(x^2",", x > 1):}`
Determine whether the following function is differentiable at the indicated values.
f(x) = |x2 – 1| at x = 1
Determine whether the following function is differentiable at the indicated values.
f(x) = sin |x| at x = 0
Show that the following functions are not differentiable at the indicated value of x.
`f(x) = {{:(-x + 2, x ≤ 2),(2x - 4, x > 2):}` , x = 2
Show that the following functions are not differentiable at the indicated value of x.
`f(x) = {{:(3x",", x < 0),(-4x",", x ≥ 0):}` , x = 0
The graph of f is shown below. State with reasons that x values (the numbers), at which f is not differentiable.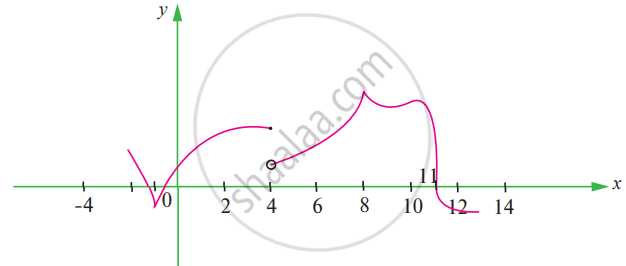
If f(x) = |x + 100| + x2, test whether f’(–100) exists.
Examine the differentiability of functions in R by drawing the diagram
|cos x|
Choose the correct alternative:
f y = f(x2 + 2) and f'(3) = 5 , then `("d"y)/("d"x)` at x = 1 is
Choose the correct alternative:
If y = mx + c and f(0) = f’(0) = 1, then f(2) is
Choose the correct alternative:
If f(x) = x + 2, then f'(f(x)) at x = 4 is
Choose the correct alternative:
If pv = 81, then `"dp"/"dv"` at v = 9 is
Choose the correct alternative:
If g(x) = (x2 + 2x + 1) f(x) and f(0) = 5 and `lim_(x -> 0) (f(x) - 5)/x` = 4, then g'(0) is
Choose the correct alternative:
If f(x) = `{{:(x + 2, - 1 < x < 3),(5, x = 3),(8 - x, x > 3):}` , then at x = 3, f'(x) is
