Advertisements
Advertisements
प्रश्न
दो पासों पर क्रमशः 1, 2, 3, 4, 5, 6 और 1, 1, 2, 2, 3, 3 संख्याएँ लिखी हुई हैं। इनको एक साथ फेंका जाता है तथा इन पर आई संख्याओं का योग लिख लिया जाता है। इसकी प्रायिकता ज्ञात कीजिए कि अलग-अलग प्रत्येक योग 2 से 9 तक हो।
उत्तर
कुल परिणामों की संख्या = 36
(i) मान लीजिए E1 = योग 2 प्राप्त होने की घटना = {(1, 1), (1, 1)}
∴ n(E1) = 2
∴ `P(E_1) = (n(E_1))/(n(S)) = 2/36 = 1/8`
(ii) मान लीजिए E2 = योग 3 प्राप्त होने की घटना = {(1, 2), (1, 2), (2, 1), (2, 1)}
∴ n(E2) = 4
∴ `P(E_2) = (n(E_2))/(n(S)) = 4/36 = 1/9`
(iii) मान लीजिए E3 = योग 4 प्राप्त होने की घटना = {(2, 2), (2, 2), (3, 1), (3, 1), (1, 3), (1, 3)}
∴ n(E3) = 6
∴ `P(E_3) = (n(E_3))/(n(S)) = 6/36 = 1/6`
(iv) मान लीजिए E4 = योग 5 प्राप्त होने की घटना = {(2, 3), (2, 3), (4, 1), (4, 1), (3, 2), (3, 2)}
∴ n(E4) = 6
∴ `P(E_4) = (n(E_4))/(n(S)) = 6/36 = 1/6`
(v) मान लीजिए E5 = योग 6 प्राप्त होने की घटना = {(3, 3), (3, 3), (4, 2), (4, 2), (5, 1), (5, 1)}
∴ n(E5) = 6
∴ `P(E_5) = (n(E_5))/(n(S)) = 6/36 = 1/6`
(vi) मान लीजिए E6 = योग 7 प्राप्त होने की घटना = {(4, 3), (4, 3), (5, 2), (5, 2), (6, 1), (6, 1)}
∴ n(E6) = 6
∴ `P(E_6) = (n(E_6))/(n(S)) = 6/36 = 1/6`
(vii) मान लीजिए E7 = योग 8 प्राप्त होने की घटना = {(5, 3), (5, 3), (6, 2), (6, 2)}
∴ n(E7) = 4
∴ `P(E_7) = (n(E_7))/(n(S)) = 4/36 = 1/9`
(viii) मान लीजिए E8 = योग 9 प्राप्त होने की घटना = {(6, 3), (6, 3)}
∴ n(E8) = 2
∴ `P(E_8) = (n(E_8))/(n(S)) = 2/36 = 1/18`
APPEARS IN
संबंधित प्रश्न
एक पत्ता 52 ताश के पत्तों के अच्छी तरह से फेंटे गए गड्डी में से निकाला जाता है। लाल रंग का तस्वीर वाला पत्ता प्राप्त करने की प्रायिकता ज्ञात कीजिए।
एक पासे के फलकों पर संख्याएँ 1, 2, 2, 3, 3 और 6 लिखी हुई हैं। इसे दो बार फेंका जाता है तथा दोनों बार प्राप्त हुई संख्याओं के योग लिख लिए जाते हैं। दोनों बार फेंकने के बाद प्राप्त योग के सम्भावित कुछ मान निम्नलिखित सारणी में दिए हैं। इस सारणी को पूरा कीजिए
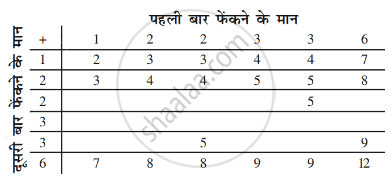
इसकी क्या प्रायिकता है कि कुल योग
(i) एक सम संख्या होगा?
(ii) 6 है?
(iii) कम-से-कम 6 है?
एक जार में 24 कंचे हैं जिनमें कुछ हरे हैं और शेष नीले हैं। यदि इस जार में से यादृच्छया एक कंचा निकाला जाता है, तो इस कंचे के हरा होने की प्रायिकता `2/3` है। जार में नीले कंचों की संख्या ज्ञात कीजिए।
निम्नलिखित प्रयोग में से वाक्य प्रयोग के परिणाम समप्रायिक हैं। स्पष्ट कीजिए।
एक खिलाड़ी बास्केटबॉल को बास्केट में डालने का प्रयत्न करती है। वह बास्केट में बॉल डाल पाती है या नहीं डाल पाती है।
जब हम किसी सिक्के को उछालते हैं, तो दो संभव परिणाम हैं– चित या पट। अत:, इनमें से प्रत्येक परिणाम की प्रायिकता `1/2` है। अपने उत्तर का औचित्य दीजिए।
दो पासों को एक साथ फेंका जाता है। निम्नलिखित प्राप्त करने की प्रायिकता ज्ञात कीजिए:
दोनों पासों पर भिन्न-भिन्न संख्याएँ।
दो पासों को एक साथ फेंका जाता है। इसकी क्या प्रायिकता है कि दोनों पासों पर आयी संख्याओं का योग 1 हो?
दो पासों को एक साथ फेंका जाता है। इसकी प्रायिकता ज्ञात कीजिए कि पासों पर आयी संख्याओं का गुणनफल 6 है।
दो पासों को एक साथ फेंका जाता है। इसकी प्रायिकता ज्ञात कीजिए कि पासों पर आयी संख्याओं का गुणनफल 7 है।
एक सिक्के को 3 बार उछाला जाता है। संभव परिणामों की एक सूची बनाइए। निम्नलिखित प्राप्त करने की प्रायिकता ज्ञात कीजिए:
न्यूनतम 2 चित
