Advertisements
Advertisements
प्रश्न
दो ठोस शंकुओं को एक बेलनाकार नली में आकृति में दर्शाए अनुसार रखा जाता है। इनकी धारिताओं का अनुपात 2:1 है। इन शंकुओं की ऊँचाइयाँ और धारिताएँ ज्ञात कीजिए। बेलन के शेष भाग का आयतन भी ज्ञात कीजिए।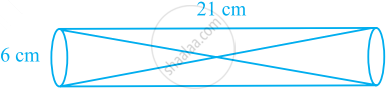
उत्तर
माना शंकु A का आयतन 2V और शंकु B का आयतन V है।
पुनः, मान लीजिए शंकु A की ऊँचाई = h1 cm,
फिर शंकु B की ऊँचाई = (21 – h1) cm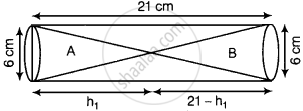
दिया गया है, शंकु का व्यास = 6 cm
∴ शंकु की त्रिज्या = `6/2` = 3 cm
अब, शंकु का आयतन,
A = 2V
= `1/3 pi"r"^2"h"`
= `1/3 pi(3)^2"h"_1`
⇒ V = `1/6 pi9"h"_1`
= `3/2 "h"_1pi` ...(i)
और शंकु का आयतन,
B = V
= `1/3 pi(3)^2(21 - "h"_1)`
= 3π(21 – h1) ...(ii)
समीकरण (i) और (ii) से,
`3/2 "h"_1 pi` = 3π(21 – h1)
⇒ h1 = 2(21 – h1)
⇒ 3h1 = 42
⇒ h1 = `42/3` = 14 cm
∴ शंकु की ऊँचाई
B = 21 – h1
= 21 – 14
= 7 cm
अब, शंकु का आयतन,
A = `3 xx 14 xx 22/7` = 132 cm2 ...[समीकरण (i) का उपयोग करके]
और शंकु का आयतन,
B = `1/3 xx 22/7 xx 9 xx 7` = 66 cm3 ...[समीकरण (ii) का उपयोग करके]
अब, बेलन का आयतन
= πr2h
= `22/7 (3)^2 xx 21`
= 594 cm3
∴ शेष भाग का आवश्यक आयतन
= बेलन का आयतन – (शंकु A का आयतन + शंकु B का आयतन)
= 594 – (132 + 66)
= 396 cm3
APPEARS IN
संबंधित प्रश्न
एक खिलौना त्रिज्या 3.5 सेमी वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्धगोले पर अध्यारोपित है। इस खिलौने की संपूर्ण ऊँचाई 15.5 सेमी है। इस खिलौने का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। [प्रयोग करें π = `22/7`]
एक ठोस एक अर्धगोले पर खड़े एक शंकु के आकार का है जिनकी त्रिज्याएँ 1 सेमी हैं तथा शंकु की ऊँचाई उसकी त्रिज्या के बराबर है। इस ठोस का आयतन π के पदों में ज्ञात कीजिए।
एक बर्तन एक उल्टे शंकु के आकार का है। इसकी ऊँचाई 8 सेमी है और इसके ऊपरी सिरे (जो खुला हुआ है) की त्रिज्या 5 सेमी है। यह ऊपर तक पानी से भरा हुआ है। जब इस बर्तन में सीसे की कुछ गोलियाँ जिनमें प्रत्येक 0.5 सेमी त्रिज्या वाला एक गोला है, डाली जाती है, तो इसमें से भरे हुए पानी का एक चौथाई भाग बाहर निकल जाता है। बर्तन में डाली गई सीसे की गोलियों की संख्या ज्ञात कीजिए।
एक ठोस में, ऊँचाई 120 सेमी और त्रिज्या 60 सेमी वाला एक शंकु सम्मिलित है, जो 60 सेमी त्रिज्या वाले एक अर्धगोले पर आरोपित है। इस ठोस को पानी से भरे हुए एक लंब वृत्तीय बेलन में इस प्रकार सीधा डाल दिया जाता है कि यह बेलन की तली को स्पर्श करे। यदि बेलन की त्रिज्या 60 सेमी और और ऊँचाई 180 सेमी है तो बेलन में शेष बचे पानी का आयतन ज्ञात कीजिए। [π = `22/7`] का प्रयोग करें
आधार व्यास 2 cm और ऊँचाई 16 cm वाले धातु के एक ठोस बेलन को पिघला कर समान माप के बारह ठोस गोले बनाये जाते हैं। प्रत्येक गोले का व्यास ______ है।
विमाओं 9 cm × 11 cm × 12 cm वाले एक सीसे के घनाभाकार ठोस से 3 cm व्यास वाली कितनी गोलियाँ बनायी जा सकती हैं?
एक 7 cm व्यास वाले बेलनाकार बीकर, जिसमें कुछ पानी भरा है, में 1.4 cm व्यास वाले कंचे डाले जाते हैं। कंचों की वह संख्या ज्ञात कीजिए जिनको बीकर में डालने से पानी का स्तर 5.6 cm ऊपर उठ जायेगा।
24 m लंबी, 0.4 m मोटी और 6 m ऊँची एक दीवार का ईंटों से निर्माण कराया जाता है, जिनमें से प्रत्येक ईंट की विमाएँ 25 cm × 16 cm × 10 cm हैं। यदि दीवार के आयतन का `1/10` भाग मसाले से भरा जाता है, तो दीवार के निर्माण में लगने वाली ईंटों की संख्या ज्ञात कीजिए।
आधार 11 m × 6 m वाले एक घनाभाकार पानी की टंकी में 5 m की ऊँचाई तक पानी भरा है। यदि इस पानी को 3.5 m त्रिज्या वाली एक बेलनाकार टंकी में स्थानांतरित कर दिया जाये, तो इस बेलनाकार टंकी में पानी के स्तर की ऊँचाई ज्ञात कीजिए।
चावलों की एक ढेरी 9 m व्यास और 3.5 m ऊँचाई वाले एक शंकु के आकार की है। इन चावलों का आयतन ज्ञात कीजिए। इस ढेरी को केवल ढकने मात्र के लिए कितने कैनवस कपड़े की आवश्यकता होगी ?
