Advertisements
Advertisements
प्रश्न
Draw a tangent to the circle from the point P having radius 3.6 cm, and centre at O. Point P is at a distance 7.2 cm from the centre.
उत्तर
Radius = 3.6, Distance = 7.2 cm.

Steps of construction:
1. With O as centre, draw a circle of radius 3.6 cm.
2. Draw a line OP = 7.2 cm.
3. Draw a perpendicular bisector of OP which cuts OP at M.
4. With M as centre and MO as radius draw a circle which cuts the previous circle at A and B.
5. Join AP and BP, AP and BP are the required tangents.
Length of the tangents PA = PB = 6.26 cm
Verification: In the right triangle ∆OAP
PA2 = OP2 – OA2
= 7.22 – 3.62
= (7.2 + 3.6) (7.2 – 3.6)
PA2 = 10.8 × 3.6
= `sqrt(38.38)`
PA = 6.2 cm
Length of the tangent = 6.2 cm
APPEARS IN
संबंधित प्रश्न
A tangent ST to a circle touches it at B. AB is a chord such that ∠ABT = 65°. Find ∠AOB, where “O” is the centre of the circle.
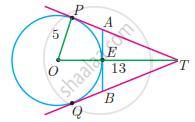
O is the centre of the circle with radius 5 cm. T is a point such that OT = 13 cm and OT intersects the circle E, if AB is the tangent to the circle at E, find the length of AB.
Two circles with centres O and O’ of radii 3 cm and 4 cm, respectively intersect at two points P and Q, such that OP and O’P are tangents to the two circles. Find the length of the common chord PQ.
Draw a tangent at any point R on the circle of radius 3.4 cm and centre at P?
Draw a circle of radius 4.5 cm. Take a point on the circle. Draw the tangent at that point using the alternate segment theorem
Draw the two tangents from a point which is 10 cm away from the centre of a circle of radius 5 cm. Also, measure the lengths of the tangents.
Draw the two tangents from a point which is 5 cm away from the centre of a circle of diameter 6 cm. Also, measure the lengths of the tangents.
A tangent is perpendicular to the radius at the
The two tangents from an external points P to a circle with centre at O are PA and PB. If ∠APB = 70° then the value of ∠AOB is
CP and CQ are tangents to a circle with centre at 0. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 7 cm, then the length of BR is