Advertisements
Advertisements
प्रश्न
Two circles with centres O and O’ of radii 3 cm and 4 cm, respectively intersect at two points P and Q, such that OP and O’P are tangents to the two circles. Find the length of the common chord PQ.
उत्तर
In ∆OO’P
(O’O)2 = OP2 + O’P2
= 32 + 42

= 9 + 16
(OO’)2 = 25
∴ OO’ = 5 cm
Since the line joining the centres of two intersecting circles is perpendicular bisector of their common chord.
OR ⊥ PQ and PR = RQ
Let OR be x, then O’R = 5 – x again Let PR = RQ = y cm
In ∆ORP,
OP2 = OR2 + PR2
9 = x2 + y2 ...(1)
In ∆O’RP,
O’P2 = O’R2 + PR2
16 = (5 – x)2 + y2
16 = 25 + x2 – 10x + y2
16 = x2 + y2 + 25 – 10x
16 = 9 + 25 – 10x ...[From (1)]
16 = 34 – 10x
10x = 34 – 16 = 18
x = `18/10` = 1.8 cm
Substitute the value of x = 1.8 in (1)
9 = (1.8)2 + y2
y2 = 9 – 3.24
y2 = 5.76
y = `sqrt(5.76)` = 2.4 cm
Hence PQ = 2(2.4) = 4.8 cm
Length of the common chord PQ = 4.8 cm
APPEARS IN
संबंधित प्रश्न
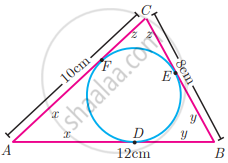
A circle is inscribed in ∆ABC having sides 8 cm, 10 cm and 12 cm as shown in the figure, Find AD, BE and CF.
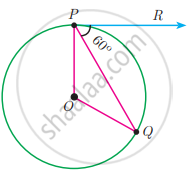
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120°. Find ∠OPQ.
In two concentric circles, a chord of length 16 cm of larger circle becomes a tangent to the smaller circle whose radius is 6 cm. Find the radius of the larger circle
Draw a circle of radius 4.5 cm. Take a point on the circle. Draw the tangent at that point using the alternate segment theorem
Draw the two tangents from a point which is 10 cm away from the centre of a circle of radius 5 cm. Also, measure the lengths of the tangents.
Take a point which is 11 cm away from the centre of a circle of radius 4 cm and draw the two tangents to the circle from that point.
How many tangents can be drawn to the circle from an exterior point?
The two tangents from an external points P to a circle with centre at O are PA and PB. If ∠APB = 70° then the value of ∠AOB is
CP and CQ are tangents to a circle with centre at 0. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 7 cm, then the length of BR is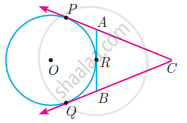
If PR is tangent to the circle at P and O is the centre of the circle, then ∠POQ is