Advertisements
Advertisements
प्रश्न
Show that the angle bisectors of a triangle are concurrent
उत्तर
Given: ABC is a triangle. AD, BE and CF are the angle bisector of ∠A, ∠B, and ∠C.
To Prove: Bisector AD, BE and CF intersect
Proof: The angle bisectors AD and BE meet at O.
Assume CF does not pass through O. By angle bisector theorem.
AD is the angle bisector of ∠A
`"BD"/"DC" = "AB"/"AC"` ...(1)
BE is the angle bisector of ∠B

`"CE"/"EA" = "BC"/"AB"` ...(2)
CF is the angle bisector ∠C
`"AF"/"FB" = "AC"/"BC"` ...(3)
Multiply (1) (2) and (3)
`"BD"/"DC" xx "CE"/"EA" xx "AF"/"FB" = "AB"/"AC" xx "BC"/"AB" xx "AC"/"BC"`
So by Ceva’s theorem.
The bisector AD, BE and CF are concurrent.
APPEARS IN
संबंधित प्रश्न
An artist has created a triangular stained glass window and has one strip of small length left before completing the window. She needs to figure out the length of left out portion based on the lengths of the other sides as shown in the figure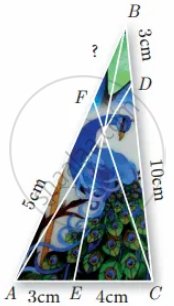
O is any point inside a triangle ABC. The bisector of ∠AOB, ∠BOC and ∠COA meet the sides AB, BC and CA in point D, E and F respectively. Show that AD × BE × CF = DB × EC × FA
Let ABC be a triangle and D, E, F are points on the respective sides AB, BC, AC or their extensions. Let AD : DB = 5 : 3, BE : EC = 3 : 2 and AC = 21 . Find the length of the line segment CF
