Advertisements
Advertisements
प्रश्न
O is any point inside a triangle ABC. The bisector of ∠AOB, ∠BOC and ∠COA meet the sides AB, BC and CA in point D, E and F respectively. Show that AD × BE × CF = DB × EC × FA
उत्तर
In ∆ABC the bisector meets AB at D, BC at E and AC at F.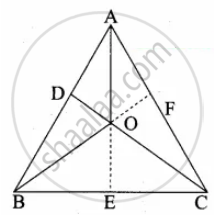
The angle bisector AO, BO and CO intersect at “O”.
By Cevas Theorem
`"AD"/"DB" xx "BF"/"EC" xx "CF"/"AF"` = 1
AD × BE × CF = DB × EC × AF
Hence it is proved
APPEARS IN
संबंधित प्रश्न
Show that the angle bisectors of a triangle are concurrent
An artist has created a triangular stained glass window and has one strip of small length left before completing the window. She needs to figure out the length of left out portion based on the lengths of the other sides as shown in the figure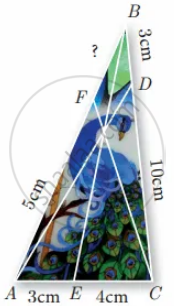
Let ABC be a triangle and D, E, F are points on the respective sides AB, BC, AC or their extensions. Let AD : DB = 5 : 3, BE : EC = 3 : 2 and AC = 21 . Find the length of the line segment CF
