Advertisements
Advertisements
प्रश्न
Draw the graph of y = | x | + 2.
उत्तर
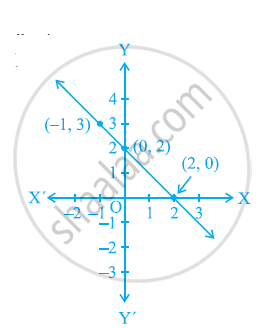
We have
y = | x | + 2 ............. (1)
Putting x = 0 , we get y = 2 ..............
Putting x = 1 , we get y = 3
Putting x = - 1 , we get y = 3
Thus, the we have the following table for the points on graph of | x | + 2
| x | 0 | 1 | 1 |
| y | 2 | 3 | 3 |
Graph of line equation y = | x | + 2

APPEARS IN
संबंधित प्रश्न
From the choices given below, choose the equation whose graphs are given in the given figures.
For the first figure
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x

For the second figure
(i) y = x +2
(ii) y = x − 2
(iii) y = − x + 2
(iv) x + 2y = 6
If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance travelled by the body is
(i) 2 units (ii) 0 unit
Draw the graph of the equation given below. Also, find the coordinates of the point
where the graph cuts the coordinate axes : 2x + y = 6
Draw the graph of the equation
4x + 3y + 6 = 0
From the graph, find :
(i) y1, the value of y, when x = 12.
(ii) y2, the value of y, when x = - 6.
Draw the graph (straight line) given by equation x - 3y = 18. If the straight line is drawn passes through the points (m, - 5) and (6, n); find the values of m and n.
Solve, graphically, the following pairs of equation :
x - 5 = 0
y + 4 = 0
The point (0, 3) lies on the graph of the linear equation 3x + 4y = 12.
The graph given below represents the linear equation x = 3 (see figure).

The graph of every linear equation in two variables need not be a line.
The force exerted to pull a cart is directly proportional to the acceleration produced in the body. Express the statement as a linear equation of two variables and draw the graph of the same by taking the constant mass equal to 6 kg. Read from the graph, the force required when the acceleration produced is (i) 5 m/sec2, (ii) 6 m/sec2.
