Advertisements
Advertisements
प्रश्न
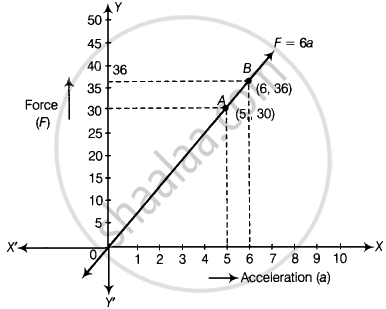
The force exerted to pull a cart is directly proportional to the acceleration produced in the body. Express the statement as a linear equation of two variables and draw the graph of the same by taking the constant mass equal to 6 kg. Read from the graph, the force required when the acceleration produced is (i) 5 m/sec2, (ii) 6 m/sec2.
उत्तर
Given that, the force (F) is directly proportional to the acceleration (a).
i.e., F ∞ a
⇒ F = ma ...[Where, m = arbitrary constant and take value 6 kg of mass]
∴ F = 6a ...(i)
(i) If a 5 m/s2, then from equation (i), we get
F = 6 × 5 = 30 N
(ii) If a 6 m/s2, then from equation (i), we get
F = 6 × 6 = 36 N
Here, we find two points A(5, 30) and B(6, 36).
So draw the graph by plotting the points and joining the line AB.
APPEARS IN
संबंधित प्रश्न
Draw the graph of the following linear equations in two variables:- y = 3x
The taxi fare in a city is as follows:- For the first kilometre, the fare is Rs. 8 and for the subsequent distance it is Rs. 5 per km. Taking the distance covered as x km and total fare as Rs y, write a linear equation for this information, and draw its graph.
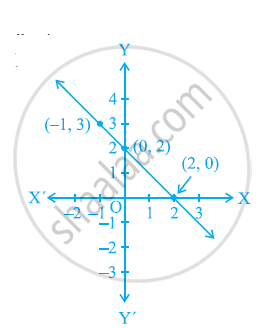
From the choices given below, choose the equation whose graphs are given in the given figures.
For the first figure
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x

For the second figure
(i) y = x +2
(ii) y = x − 2
(iii) y = − x + 2
(iv) x + 2y = 6
Draw the graph of the following linear equation in two variable : y = 2x
Draw the graph of the following linear equation in two variable : 3x + 5y = 15
Plot the points (3, 5) and (− 1, 3) on a graph paper and verify that the straight line passing
through these points also passes through the point (1, 4).
Draw the graph for the equation, given below :
x + 5 = 0
Draw the graph for the equation, given below :
3x + 2y = 6
Draw the graph obtained from the table below:
| X | a | 3 | - 5 | 5 | c | - 1 |
| Y | - 1 | 2 | b | 3 | 4 | 0 |
Use the graph to find the values of a, b and c. State a linear relation between the variables x and y.
Write the linear equation such that each point on its graph has an ordinate 3 times its abscissa.
